- (問題1)
以下のプログラムを作成せよ.
"S:\a.txt" を "wt" モードで開く.
そのファイルが開けなかったら,
perror("file can not open");
exit(1);
を実行する.
開けたら,そのファイルに
double x[4], y[4];
x[0]=0.0; y[0]=0.0;
x[1]=1.0; y[1]=0.0;
x[2]=1.0; y[2]=1.0;
x[3]=0.0; y[3]=1.0;
fprintf( fp, "%lf\t%lf\n", x[0], y[0]);
fprintf( fp, "%lf\t%lf\n", x[1], y[1]);
fprintf( fp, "%lf\t%lf\n", x[2], y[2]);
fprintf( fp, "%lf\t%lf\n", x[3], y[3]);
fprintf( fp, "%lf\t%lf\n", x[0], y[0]);
と,書き込む.
そして,ファイルを閉じる.
ただし,fp は "S:\a.txt" のファイルポインタ.
C言語上では"S:\\a.txt"となることに注意せよ.
fprintf内の "\t" はタブ文字である.
そして,そのプログラムを実行し,
できあがった"S:\a.txt" をエクセルで開き,
散布図(マーカーなし,線あり)でグラフにせよ.
ヒント:
・正方形型に表示される.
・エクセルやサクラエディタで "S:\a.txt" を開いている状態で,
同ファイルを "wt" モードで開こうとすると失敗する.
- (問題2)
以下のプログラムを作成せよ.
"S:\a.txt" を "wt" モードで開き,(開けなかった 問題1 と同様)
そのファイルに
x = 0.0 かつ y = sin(x) の状態で,
fprintf( fp, "%lf\t%lf\n", x, y);
と書き込む.
x = 0.1 かつ y = sin(x) の状態で,
fprintf( fp, "%lf\t%lf\n", x, y);
と書き込む.
x = 0.2, y = sin(x) で fprintf( fp, "%lf\t%lf\n", x, y);
x = 0.3, y = sin(x) で fprintf( fp, "%lf\t%lf\n", x, y);
x = 0.4, y = sin(x) で fprintf( fp, "%lf\t%lf\n", x, y);
:
x = 9.9, y = sin(x) で fprintf( fp, "%lf\t%lf\n", x, y);
そして,ファイルを閉じる.
また,三角関数のsinを用いるために,
プログラムの先頭近辺(#includeの直後)に
#include <math.h>
を記述せよ.
できあがったファイルを エクセルで開き,
散布図でグラフにせよ.
- (問題3)
座標(x0, y0)を,原点を中心にθだけ回転した
座標(x1, y1)は,
x1 = cos(θ)*x0 + sin(θ)*y0;
y1 = -sin(θ)*x0 + cos(θ)*y0;
で,求めることができる.
以下のプログラムを作成せよ.
double x[4], y[4];
x[0]=0.0; y[0]=0.0;
x[1]=1.0; y[1]=0.0;
x[2]=1.0; y[2]=1.0;
x[3]=0.0; y[3]=1.0;
とする.
"S:\a.txt" を開き,
( x[0], y[0] )を θ=0.1 だけ回転した座標を
"%lf\t%lf\n"の フォーマットでファイルに書き込む.
( x[1], y[1] )を θ=0.1 だけ回転した座標を書き込む.
( x[2], y[2] )を θ=0.1 だけ回転した座標を書き込む.
( x[3], y[3] )を θ=0.1 だけ回転した座標を書き込む.
( x[0], y[0] )を θ=0.1 だけ回転した座標を書き込む.
そして,ファイルを閉じる.
できあがったファイルを エクセルで開き,
散布図でグラフにせよ.
- (問題4)
以下のプログラムを作成せよ.
double x[4], y[4];
x[0]=0.0; y[0]=0.0;
x[1]=1.0; y[1]=0.0;
x[2]=1.0; y[2]=1.0;
x[3]=0.0; y[3]=1.0;
とする.
"S:\a.txt" を開き,
x[0], y[0] を θ=0.0 だけ回転した座標,
x[1], y[1] を θ=0.0 だけ回転した座標,
x[2], y[2] を θ=0.0 だけ回転した座標,
x[3], y[3] を θ=0.0 だけ回転した座標,
x[0], y[0] を θ=0.0 だけ回転した座標,
空行
を書き込む.
x[0], y[0] を θ=0.1 だけ回転した座標,
x[1], y[1] を θ=0.1 だけ回転した座標,
x[2], y[2] を θ=0.1 だけ回転した座標,
x[3], y[3] を θ=0.1 だけ回転した座標,
x[0], y[0] を θ=0.1 だけ回転した座標,
空行
を書き込む.
x[0], y[0] を θ=0.2 だけ回転した座標,
x[1], y[1] を θ=0.2 だけ回転した座標,
x[2], y[2] を θ=0.2 だけ回転した座標,
x[3], y[3] を θ=0.2 だけ回転した座標,
x[0], y[0] を θ=0.2 だけ回転した座標,
空行
を書き込む.
x[0], y[0] を θ=0.3 だけ回転した座標,
x[1], y[1] を θ=0.3 だけ回転した座標,
x[2], y[2] を θ=0.3 だけ回転した座標,
x[3], y[3] を θ=0.3 だけ回転した座標,
x[0], y[0] を θ=0.3 だけ回転した座標,
空行
を書き込む.
;
x[0], y[0] を θ=0.9 だけ回転した座標,
x[1], y[1] を θ=0.9 だけ回転した座標,
x[2], y[2] を θ=0.9 だけ回転した座標,
x[3], y[3] を θ=0.9 だけ回転した座標,
x[0], y[0] を θ=0.9 だけ回転した座標,
空行
を書き込む.
そして,ファイルを閉じる.
できあがったファイルを エクセルで開き,
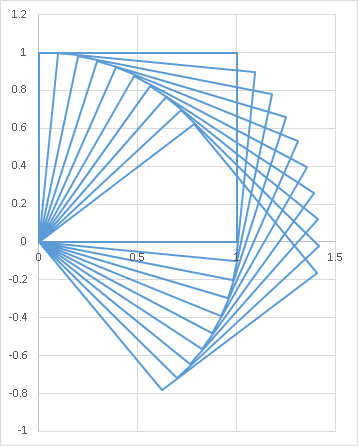
散布図でグラフにせよ.
ヒント:エクセルでは,空行があるとそこで線が途切れる
できあがる絵は このような感じになる.
 - (問題5)
コッホ曲線を描くプログラムを作成せよ.
- (問題5)
コッホ曲線を描くプログラムを作成せよ.
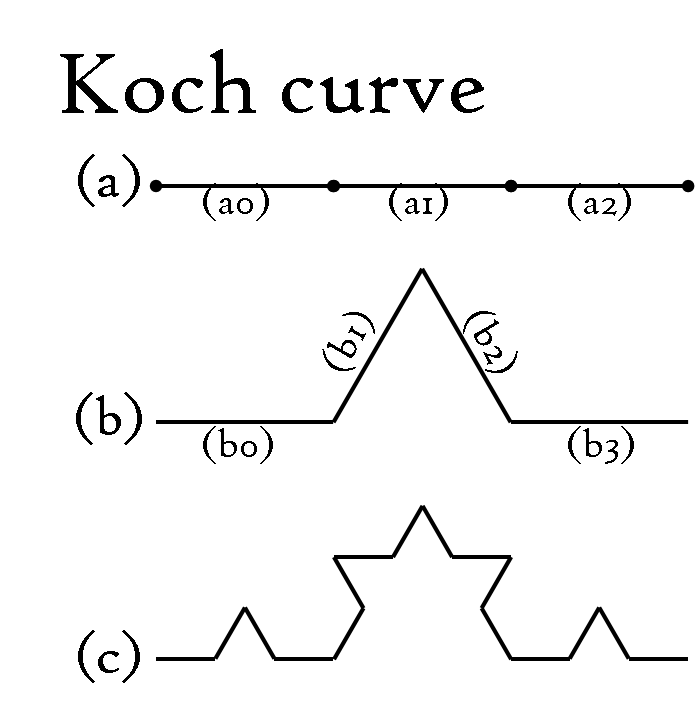 コッホ曲線は,以下の様に作成できる.
・(a)の様な線分を描く.
・(a)を3等分し,
中央の線(a1)を辺とする正三角形を描く(図の(b1)や(b2)を描く).
・代わりに(a1)を消して,(b)の状態(4本の線)にする.
・(b)の状態の4本の各線に,上記の「3等分,正三角形を足す,元の線を消す」を行い,
(c)の状態にする.
・(c)の状態の各線(16本)に,「3等分,正三角形を足す,元の線を消す」を行い,64本にする.
以下同様に繰り返す.
例
コッホ曲線は,以下の様に作成できる.
・(a)の様な線分を描く.
・(a)を3等分し,
中央の線(a1)を辺とする正三角形を描く(図の(b1)や(b2)を描く).
・代わりに(a1)を消して,(b)の状態(4本の線)にする.
・(b)の状態の4本の各線に,上記の「3等分,正三角形を足す,元の線を消す」を行い,
(c)の状態にする.
・(c)の状態の各線(16本)に,「3等分,正三角形を足す,元の線を消す」を行い,64本にする.
以下同様に繰り返す.
例
.png)
.png)
.png) 再帰を用いて,コッホ曲線の座標をファイルに出力する関数
void koch(double x0, double y0, double x1, double y1, int n, FILE *fp);
を作成し,それをmain関数より呼び出し,エクセルで表示せよ.
ただし,引数の(x0, y0)は,コッホ曲線を描く始点,
引数の(x1, y1)は,コッホ曲線の終点.
int n は再帰の深さを表す.
n==0 なら これ以上再帰せず,
座標(x0,y0)と座標(x1,y1)をファイルfpに出力する.
0<n なら (x0,y0)-(x1,y1) の線分を3等分し,4個の線分に変換し,
それぞれに koch() を再帰的に呼び出す.
その際,第5引数は n-1 に変更する.
円周率πを用いるためには,
プログラムの先頭近辺(#includeの直後)に
#define _USE_MATH_DEFINES // for C++
#include <cmath>
を記述し,M_PI を用いる.
例:x = sin( M_PI/3.0 );
平方根を用いるには,
プログラムの先頭近辺(#includeの直後)に
#include <math>
を記述し,sqrt() を用いる.
例:x = sqrt( 3.0 )/2.0;
ヒント:
main関数でファイルを開き,koch関数には fp を渡す.
再帰を用いて,コッホ曲線の座標をファイルに出力する関数
void koch(double x0, double y0, double x1, double y1, int n, FILE *fp);
を作成し,それをmain関数より呼び出し,エクセルで表示せよ.
ただし,引数の(x0, y0)は,コッホ曲線を描く始点,
引数の(x1, y1)は,コッホ曲線の終点.
int n は再帰の深さを表す.
n==0 なら これ以上再帰せず,
座標(x0,y0)と座標(x1,y1)をファイルfpに出力する.
0<n なら (x0,y0)-(x1,y1) の線分を3等分し,4個の線分に変換し,
それぞれに koch() を再帰的に呼び出す.
その際,第5引数は n-1 に変更する.
円周率πを用いるためには,
プログラムの先頭近辺(#includeの直後)に
#define _USE_MATH_DEFINES // for C++
#include <cmath>
を記述し,M_PI を用いる.
例:x = sin( M_PI/3.0 );
平方根を用いるには,
プログラムの先頭近辺(#includeの直後)に
#include <math>
を記述し,sqrt() を用いる.
例:x = sqrt( 3.0 )/2.0;
ヒント:
main関数でファイルを開き,koch関数には fp を渡す.
 - (問題5)
コッホ曲線を描くプログラムを作成せよ.
- (問題5)
コッホ曲線を描くプログラムを作成せよ.
 コッホ曲線は,以下の様に作成できる.
・(a)の様な線分を描く.
・(a)を3等分し,
中央の線(a1)を辺とする正三角形を描く(図の(b1)や(b2)を描く).
・代わりに(a1)を消して,(b)の状態(4本の線)にする.
・(b)の状態の4本の各線に,上記の「3等分,正三角形を足す,元の線を消す」を行い,
(c)の状態にする.
・(c)の状態の各線(16本)に,「3等分,正三角形を足す,元の線を消す」を行い,64本にする.
以下同様に繰り返す.
例
コッホ曲線は,以下の様に作成できる.
・(a)の様な線分を描く.
・(a)を3等分し,
中央の線(a1)を辺とする正三角形を描く(図の(b1)や(b2)を描く).
・代わりに(a1)を消して,(b)の状態(4本の線)にする.
・(b)の状態の4本の各線に,上記の「3等分,正三角形を足す,元の線を消す」を行い,
(c)の状態にする.
・(c)の状態の各線(16本)に,「3等分,正三角形を足す,元の線を消す」を行い,64本にする.
以下同様に繰り返す.
例
.png)
.png)
.png) 再帰を用いて,コッホ曲線の座標をファイルに出力する関数
void koch(double x0, double y0, double x1, double y1, int n, FILE *fp);
を作成し,それをmain関数より呼び出し,エクセルで表示せよ.
ただし,引数の(x0, y0)は,コッホ曲線を描く始点,
引数の(x1, y1)は,コッホ曲線の終点.
int n は再帰の深さを表す.
n==0 なら これ以上再帰せず,
座標(x0,y0)と座標(x1,y1)をファイルfpに出力する.
0<n なら (x0,y0)-(x1,y1) の線分を3等分し,4個の線分に変換し,
それぞれに koch() を再帰的に呼び出す.
その際,第5引数は n-1 に変更する.
円周率πを用いるためには,
プログラムの先頭近辺(#includeの直後)に
#define _USE_MATH_DEFINES // for C++
#include <cmath>
を記述し,M_PI を用いる.
例:x = sin( M_PI/3.0 );
平方根を用いるには,
プログラムの先頭近辺(#includeの直後)に
#include <math>
を記述し,sqrt() を用いる.
例:x = sqrt( 3.0 )/2.0;
ヒント:
main関数でファイルを開き,koch関数には fp を渡す.
再帰を用いて,コッホ曲線の座標をファイルに出力する関数
void koch(double x0, double y0, double x1, double y1, int n, FILE *fp);
を作成し,それをmain関数より呼び出し,エクセルで表示せよ.
ただし,引数の(x0, y0)は,コッホ曲線を描く始点,
引数の(x1, y1)は,コッホ曲線の終点.
int n は再帰の深さを表す.
n==0 なら これ以上再帰せず,
座標(x0,y0)と座標(x1,y1)をファイルfpに出力する.
0<n なら (x0,y0)-(x1,y1) の線分を3等分し,4個の線分に変換し,
それぞれに koch() を再帰的に呼び出す.
その際,第5引数は n-1 に変更する.
円周率πを用いるためには,
プログラムの先頭近辺(#includeの直後)に
#define _USE_MATH_DEFINES // for C++
#include <cmath>
を記述し,M_PI を用いる.
例:x = sin( M_PI/3.0 );
平方根を用いるには,
プログラムの先頭近辺(#includeの直後)に
#include <math>
を記述し,sqrt() を用いる.
例:x = sqrt( 3.0 )/2.0;
ヒント:
main関数でファイルを開き,koch関数には fp を渡す.