スピン

スピンとは辞書風に言えば，素粒子の固有角運動量のことです。 ただし，その理解には量子論的な考え方が不可欠なのですが。

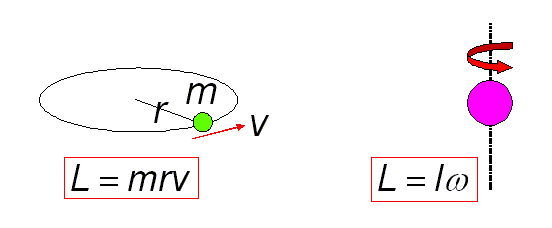
まず，「角運動量」から説明します。 運動量という言葉は高校の物理でも出てきますね。 簡単に言えば，運動量ｐは「直進的な運動の激しさ」を表す量で ｐ＝ｍｖと定義されます。つまり質量ｍと速度ｖの積です。 大学で物理を勉強した人は，角運動量についても学んだと 思います。 簡単に言えば，角運動量Ｌは「回転的な運動の激しさ」を表す量です。 例えば，質量ｍの粒子が速さｖで半径ｒの円軌道を運動しているとすると， そのときの角運動量はＬ＝ｍｒｖとなります。 あるいは，大きさを持った変形しない物体，つまり剛体が，重心を 中心として自分自身が自転していると，角運動量は Ｌ＝Ｉωとなります。ここでＩは剛体の慣性モーメント， ωは角速度です。（追加説明：慣性モーメントとは， 例えば，質量がｍで半径がｒの一様な球の慣性モーメントは I=(2/5)mr2です。角速度ですが， 円運動の場合，ｖ＝ｒωです。） 「素粒子の固有角運動量」はどちらかと言えば， 自分自身が自転している様子ですから，イメージ的には 後者のほうに近いでしょう。ただし，これは あくまでも初歩的なイメージであって正確ではありませんが。

上記では煩雑さを避けるため略していますが，運動量も角運動量 もいずれも向きを持つ量，つまりベクトルの物理量であることに 注意してください。 運動量ベクトルはもちろん速度ベクトルの方向を向いています。 直感的に言うと，角運動量ベクトルは回転軸の方向を向いています。

角運動量Ｌの単位を確認します。Ｌ＝ｍｒｖですから， 単位は ｋｇ・ｍ・（ｍ／ｓ）＝Ｊ・ｓ （ジュール・秒）です。 量子力学で出てくる基本定数としてプランク定数というものが あります。

プランク定数＝ｈ＝6.626×10-34 Js
このプランク定数が素粒子のスピンを測る単位にもなっています。 これを２πで割ったものをＨと書きましょう。
Ｈ＝ｈ／（２π）
本当は，ｈに横棒をひいた記号で表すのですが，フォントがないので 許して下さい。

上で，素粒子のスピンのイメージを「自転」で説明しましたが， これは既に述べたように便宜的なイメージです。 なぜならば，素粒子とは，大きさを持たない「点」粒子です。 （少なくとも現在の実験技術では大きさが検出不可能である 小さい粒子です。）であればI=0ですからL=0となります。 これでは「固有角運動量」は持ちようがありません。

無理やり大きさを持たせて見ましょう。 係数を無視すれば，円軌道でも，自転でも，H=mrv となります。 速度の大きさは光速度を越えることはできません。 なるべくサイズｒを小さくしたいので，ｖ＝ｃとおきます。すると 電子の場合であれば，
m=9.11×10-31 kg
c=3.00×108 m/s
H=1.05×10-34 Js
を使うと，ｒはおよそ 10-12m となります。 電子は，これよりもはるかに小さいサイズであることが 実験的に確認されています。 （だいたい，電子は量子性から波動的にも振る舞い， そのコンプトン波長は 3.86×10-13m です。 この波長で振舞うことで半導体などの動作が理解できるのですから， それが10-12m ものサイズを持っていたら話がめちゃくちゃに なります。） 従って，スピンを自転で解釈することには 無理があります。 さきほど，素粒子のスピンは本来量子論的な立場で理解しなくてはいけない といったのはこういう意味です。

さて，素粒子がスピンを持っていることは，実験的な測定の 結果わかっていることです。 既知の素粒子は，ｓＨのスピンを持っています。ｓは数で， 整数もしくは半整数です。

スピンが，0H, 1H, 2H,... の粒子：ボース粒子（ボソン）

スピンが，(1/2)H, (3/2)H, (5/2)H,... の粒子：フェルミ粒子（フェルミオン）

このような，スピンになるべきことは，理論的にはローレンツ群の 表現論から数学的に規定されています。 つまり，素粒子が相対性理論を記述するローレンツ変換に対して， 正しく従っているとすれば，上のようなスピンの系列が数学的に 出てくるのです。

上で示したものはスピンの大きさです。 スピンは角運動量であり，角運動量はベクトル量です。 ですから，素粒子の内部状態は，そのベクトルがある軸に 対してどれだけの成分を持っているか（傾いているか）で分類され ます。普通に考えれば任意の傾きの角度をとれると考えますが， 量子力学によれば，ミクロの世界では物理量は離散的になることが 知られています。 （このあたりの説明は量子論を知らない人には不親切ですが， お許しを。ちゃんと説明するとそれだけで本１冊になる。） このため，素粒子の内部状態は，スピンｓＨを持つとき，（２ｓ＋１）個の 方向があります。

スピン０Ｈ：１つしかない

スピン(1/2)H：２つある。 (1/2)H, (-1/2)H

スピン 1H：３つある。 +1H, 0H, -1H

スピン(3/2)H：４つある。 (+3/2)H, (+1/2)H, (-1/2)H, (-3/2)H

ボソンとフェルミオンはその「統計性」が異なります。 前者はボース・アインシュタイン統計（BE統計）， 後者はフェルミ・ディラック統計（FD統計） に従います。 この２つの違いは，素粒子がとることのできる，ある微視的な状態 を考えたときに，その状態を占拠できる粒子の個数にあります。

BE統計：ある状態には任意の個数の粒子が存在できる

FD統計：ある状態に存在できる粒子は１個だけである（パウリの排他律とも言います）

両極端の表現ですね。この2種類だけが我々の世界に存在するというのは 不思議でもあります。 理論的には両者の中間となるパラ統計いうものもありますが，何分 対応する現物がありません。

上の定義だけではわかりにくいですから，実例を考えます。
問題：３つの部屋がある。ここに２名の客を泊めるとき，どのような 部屋割りが可能か。

古典統計.... ９とおり

*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
I     I     I     I  I     I     I     I  I     I     I     I
I A B I     I     I  I     I A B I     I  I     I     I A B I
I     I     I     I  I     I     I     I  I     I     I     I
*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*

*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
I     I     I     I  I     I     I     I  I     I     I     I
I  A  I  B  I     I  I  A  I     I  B  I  I     I  A  I  B  I
I     I     I     I  I     I     I     I  I     I     I     I
*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*

*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
I     I     I     I  I     I     I     I  I     I     I     I
I  B  I  A  I     I  I  B  I     I  A  I  I     I  B  I  A  I
I     I     I     I  I     I     I     I  I     I     I     I
*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
BE統計.... ６とおり
*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
I     I     I     I  I     I     I     I  I     I     I     I
I X X I     I     I  I     I X X I     I  I     I     I X X I
I     I     I     I  I     I     I     I  I     I     I     I
*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*

*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
I     I     I     I  I     I     I     I  I     I     I     I
I  X  I  X  I     I  I  X  I     I  X  I  I     I  X  I  X  I
I     I     I     I  I     I     I     I  I     I     I     I
*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
FD統計... ３とおり
*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
I     I     I     I  I     I     I     I  I     I     I     I
I  X  I  X  I     I  I  X  I     I  X  I  I     I  X  I  X  I
I     I     I     I  I     I     I     I  I     I     I     I
*=====*=====*=====*  *=====*=====*=====*  *=====*=====*=====*
上の例で，統計の違いがわかったでしょうか。 素粒子の重要な（あたりまえの）性質を理解してもらうため， 古典統計の場合を付け加えてあります。 例えば，古典統計では，ボールのようなものを並べ替えるとします。 全く同じボールでも，傷をつけたり，マジックでマークをつけたりする ことで個々は区別できます。そのようにして状態の数を数えたのが 上の例です。

これに対して，素粒子は互いにすべて同一であって，本質的に 区別できません。 電子にちょっと傷をつけて他と区別する，などということは できないのです。しかし，個々の電子に目をつけて，追い掛け回して いれば，相互に区別できるのではないかとも思えるでしょう。 ところが，そこで再び量子性が登場します。 量子論に基づく本質的な不確定性のため，個別粒子を完全に 「尾行」することは無理なのです。 例えば，十字路があって，北と南から電子が走ってきて交差点で 衝突し，東と西に飛んでいったとします。 東に飛んでいった電子はどっちから来たものですか， という問には「わからない」というのが正解です。 それは２つのスリットを使う光の干渉実験のとき， スクリーンに当たった光はどちらのスリットを通ってきたのですか， という問が意味が無いのと同じことです。

熱力学を勉強したことのある人は，上のような場合の数が エントロピーに関係していることを覚えているかも知れません。 ですから，物質の性質を調べることにより，どの統計が現実の世界で実現され ているかを調べることができます。 それぞれの統計を使って理論的に計算した結果と測定結果を 比較すると，古典統計では合わず，構成要素によりBE統計あるいは FD統計を用いた結果が合っていることが確認できました。 このような理由から，個々の素粒子は同一であって 原理的に区別することが不可能です。 また，同一性は量子論と深く結びついていることも分ります。