内 容
再帰(リカーシブ)
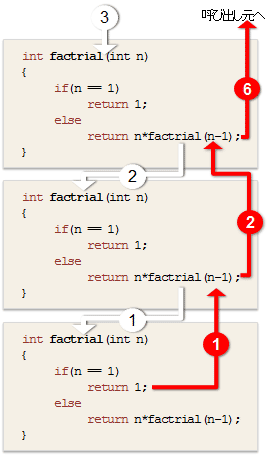
関数の中から自分自身を呼び出すことを再帰呼び出し(recursive call)と言います。例えば、階乗を求める計算を考えます。整数nの階乗は、
(a) $n=0$ の場合、$n! = 1$
(b) $n>0$ の場合、$n! = n \times (n-1)!$
となり、$n>0$の場合にはその計算式に再び階乗値を求める計算$(n-1)!$が表れます。このような再帰的な構造として定義できる処理に対して再帰関数を利用することで簡潔な表記と処理の単純化を実現することができます。
factrial.c
#include <stdio.h>
int factrial(int n)
{
if(n == 0)
return 1; // 0!=1
else
return n * factrial(n-1); // n! = n*(n-1)!
}
int main(void)
{
int n;
puts("nの階乗値を求めます。");
printf("正の整数 >> ");
scanf("%d", &n);
printf("%d\n", factrial(n));
return 0;
}
再帰の考え方
対象となる問題を、1)漸化式で表すことができる、もしくは、2)小さく分割して解を求めてから一つにまとめることで全体の解を得ることができれるのであれば、再帰呼び出しを使ってプログラムを実現することができます。漸化式で表せる例
ある数列が次の漸化式で表されているとします。
$$a_{n+1} = 2a_n + 1 ,\ a_0 = 1$$
次の項 $a_{n+1}$は、その前の項$a_n$を含んでいることから、再帰的構造を持っていると言えます。また、初項の値が1であることがわかってるので、これを再帰呼び出しの停止条件として利用することができます。
recurrence.c
#include <stdio.h>
/*
* 漸化式
* a[n+1] = 2a[n] + 1, a[0] = 1
*/
int func(int n)
{
if(n==0) //初項
return 1;
else
return 2*func(n-1) + 1;
}
int main(void)
{
int n;
printf("正の整数>> ");
scanf("%d", &n);
printf("a%d = %d\n", n,func(n));
return 0;
}
問題を小さくして解く例
問題を2つ以上の小さな問題に分けてそれぞれを再帰的に解くことができ、それらの解をまとめることで全体の解を求めます。これを分割統治法とも言います。以下は、11個の整数の要素からなる配列の最大値を求めるプログラムです。配列を中央で左右に分割し、左右のグループ毎に最大値を求めます。
binarySearch.c
#include <stdio.h>
#define N 15
/*
* 二分して最大値を求める
* @ left: 左端要素番号、right: 右端要素番号
*/
int binaryMax(int a[],int left, int right){
int mid, s1, s2;
if(left==right)
return a[left];
mid = (left + right)/2; //左右に分割する中央の要素番号
s1 = binaryMax(a, left, mid); //左グループ
s2 = binaryMax(a, mid+1, right); //右グループ
if(s1>s2) return s1; else return s2; //大きい値を戻り値とする
}
void printArray(int a[],int n)
{
int i;
for(i=0; i<n; i++) printf("%3d ", a[i]);
}
int main(void)
{
int a[] = {11,6,9,2,10,5,15,3,12,14,1,7,4,13,8};
int i;
printArray(a,N);
printf("\n");
printf("max = %d\n", binaryMax(a,0,N-1));
return 0;
}
再帰処理を実現するための条件は、
- 再帰処理における再帰関数は自分自身を呼び出していること。
- 自明なケースが存在すること(再帰呼び出し終了条件)
- 状態が自明なケースに向かっていく変化していくこと。
再帰を利用したプログラム例
かけ算
かけ算m x nは、次式のようにmをn回足した足し算の繰り返しとして書き改めることができます。
$$m \times n = m + m + \dots + m $$
さらに、かけ算を関数f(m,n)で置き換えると、次式のように表すことができます。
$$f(m,n) = f(m,n-1) + m$$
すなわち、かけ算を漸化式で表すことで、以下のような再帰呼び出しを使ったプログラムとして記述することができます。
multi.c
#include <stdio.h>
/* かけ算 m * n */
int multi(int m, int n)
{
if([[空欄ア]])
return [[空欄イ]];
else
return [[空欄ウ]];
}
int main(void)
{
int m,n;
printf("かけ算(M x N)\n");
printf("整数(M,N)>> ");
scanf("%d,%d", &m,&n);
printf("%d\n", multi(m,n));
return 0;
}
組み合わせ
n個の中からr個取り出す組み合わせ数は以下の式で求められます。
$$_nC_r = \frac{n!}{(n-r)!r!} $$
これをn個からr-1個取り出す組み合わせ数を使って書き改めると次式で表すことができます。
$$ _nC_r = _nC_{r-1} \times \frac{(n-r+1)}{r} $$
すなわち、組み合わせの数を再帰処理で求められるわけです。
combination.c
#include <stdio.h>
int comb(int n, int r)
{
if ([[空欄ア]])
return 1;
else
return [[空欄イ]]* (n-r+1)/r;
}
int main(void)
{
int n,r;
pirntf("組み合わせnCrを求めます。\n");
printf("正の整数(n,r)>> ");
scanf("%d,%d", &n,&r);
printf("%dC%d = %d\n", n,r,comb(n,r));
return 0;
}
10進2進変換
10進数を2進数に変換するためには10進数を2で割った商と剰余を求める演算を繰り返すことで求めることができます。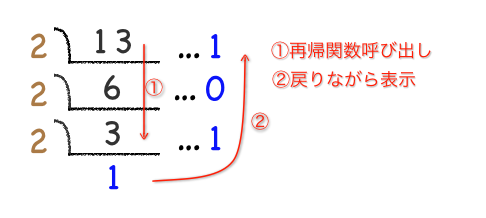
次のプログラムは、この繰り返し処理を再帰呼び出しとして実現した例です。
binary.c
#include <stdio.h>
void toBinary(int n);
int main(void)
{
int n;
printf("正の整数>> ");
scanf("%d", &n);
printf("2進表現: ");
toBinary(n);
printf("\n");
return 0;
}
void toBinary(int n)
{
if(n==0){
return;
}
else{
toBinary([[空欄ア]]);
printf("%d",n%2);
}
}
末尾再帰
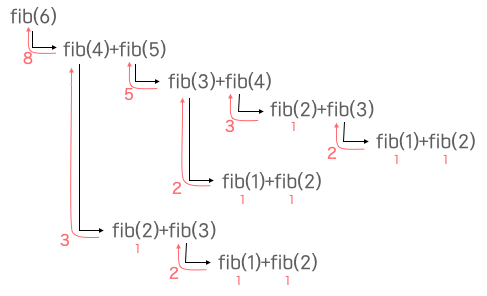
フィボナッチ数
フィボナッチ数とは、次式で表されるように
$$ F_1 = 1 $$
$$ F_2 = 1 $$
$$ F_n = F_{n-2} + F_{n-1} $$
1つ前の累算値と2つ前の累算値の和で表される数でした。これを、繰り返し処理for文を使うと、
int fibo(int n)
{
int i, fn, f1=1, f2=1;
if (n==1 || n==2){
return 1;
}
else {
for(i=0; i<n; i++){
fn = f2 + f1;
f2 = f1;
f1 = fn;
}
return fn;
}
のように、順次、一つ前と二つ前の処理結果を変数f1とf2にそれぞれ記憶させていくことで求めることができます。次に、フィボナッチ数がそれ以前と同じ処理によって得られる値を繰り返し利用していることから、再帰処理を使って、次のように書き直すことができます。
int fibo(int n)
{
if (n==1 || n==2)
return 1;
else
return fibo(n-2) + fibo(n-1);
}
末尾再帰
再帰関数の自分自身の呼び出し位置が関数の最後で再帰関数のみを呼び出すことを末尾再帰と呼びます。処理結果が戻ってくるのを待って演算するのではなく、下記のソースコードの例のように関数呼び出しの際に引数で処理結果(f1+f2)を渡していきます。
int fibo(int n, int f2, int f1)
{
if (n==1 || n==2) //停止条件
return f1;
else
return fibo(n-1,f1,f1+f2);
}
スタックオーバフロー
再帰関数の呼び出しが深くなると、すなわち呼び出し回数が多くなりすぎるとスタックオーバーフローと呼ばれる状態になり、プログラムは停止してしまいます。関数は呼び出されるとメモリのスタック領域にローカル変数や呼び出し元に戻るための戻り先(リターンアドレス)などの情報を保存し、呼び出しが終了するとその情報を破棄します。再帰関数のように、呼び出した関数から関数を呼び出す処理が繰り返されると、最初に呼び出した関数の処理が終了するまで呼び出された関数の分だけスタック領域を消費することになります。そのため、再起呼び出しが深くなりすぎた場合には、スタック領域をはみ出して他の領域のデータを壊すことになります。もし、スタックオーバーフローが問題になった場合には、for文などを使って繰り返し処理に変換します。また、末尾呼び出しの最適化機能を持つ処理系が利用できれば、再帰処理を末尾再帰に書き換えることによってスタックを回避することができます。
expand_lessBack to TOP