内 容
ハノイの塔
ハノイの塔とは三本の支柱と複数枚の中央に穴の空いた円盤からなり、ルールに従ってすべての円盤を左端の支柱から右端の支柱に移動するパズルです。円盤はすべて大きさが異なり、最初は小さい円盤が上になるように左端の支柱に収められています。円盤は一度に１枚だけ、残る２本の支柱の何れかに移動することができます。ただし、小さな円盤の上に大きな円盤を重ねることはできません。下図の左側は３枚の円盤を移動する手順です。右側は最下段の一枚を除く上段の２枚を一組の円盤として移動するとして考えた手順です。
- １）支柱Aの上段２枚一組を支柱Bへ移動
- ２）支柱Aの最下段の円盤を支柱Cへ移動
- ３）支柱Bの２枚一組を支柱Cへ移動することで完了します。
上段２枚一組についても実際には１枚ずつ移動しなければなりませんが、図の左側の手順に注目すると、
- １）支柱Aの上段１枚を支柱Cへ移動
- ２）支柱Aの中段の円盤を支柱Bへ移動
- ３）支柱Cの１枚を支柱Bへ移動
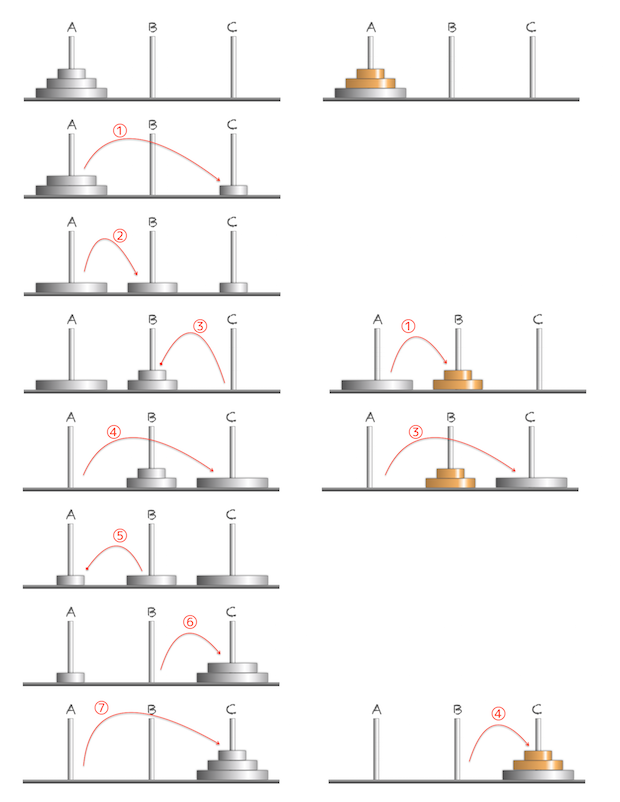
Fig.1 ハノイの塔
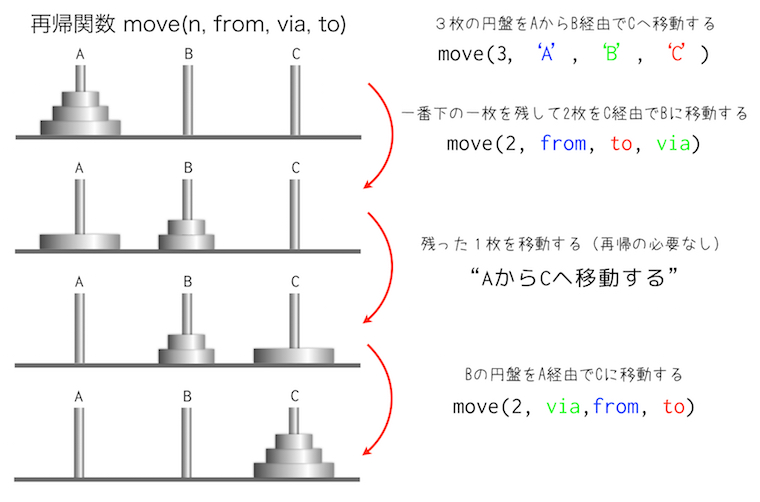
- 1) 経由地と移動先を交換して、円盤n-1枚を移動する。
- 2) n番目の円盤を現在位置から移動先へ移動する。（１枚だけなので再帰せず画面表示する）
- 3) 現在位置と移動先を交換して、円盤n-1枚を移動する。
例 hanoi.c
#include <stdio.h>
void move(int n, char from, char via, char to);
int main(void)
{
int n;
printf("円盤の枚数> ");
scanf("%d", &n);
move(n,'A','B','C');
return 0;
}
/*
* n枚の円盤をfromからvia経由でtoへ移動する
*/
void move(int n, char from, char via, char to)
{
if(n>1)
move([[空欄ア]]); //支柱Ａから支柱Bへの移動
printf("円盤%dを、%cから%cへ移動する。\n",n,from,to);
if(n>1)
move([[空欄イ]]); //支柱Bから支柱cへの移動
}
OPEN HINT
順列
n個からr個を取り出す順列のパターン数はnpr個で求められます。例えば、3個の数字1,2,3から3個取り出す順列のパターンは、[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]の6個になります。 配列を用意して各数字を要素に格納するものとして、順列を表示するプログラムを考えていきます。すべてのパターンを生成する＜重複順列＞
はじめに、無条件に数字の組み合わせパターンを表示するプログラムを考えてみます。先頭の要素を決定したら、次に2つ目の数字を決定し、・・・、と繰り返し数字を決定することで実現します。再帰呼び出しを使わない繰り返しによる順列パターンの生成
３個の数字1,2,3から３個取り出す順列パターンに限定した場合のプログラム例です。取り出す数字の個数によってfor文のネストはより深くなっていきます。
例 perm_overlap_norec.c
#include <stdio.h>
int n=3,r=3; // nPr
int p[3]; //パターンを格納する配列
int main(void)
{
int i,j,k,l;
for(i=1; i<=n; i++){
p[0] = i; //１つ目の数字
for(j=1; j<=n; j++){
p[1] = j; //２つ目の数字
for(k=1; k<=n; k++){
p[2] = k; //３つ目の数字
for(l=0; l<r; l++) printf("%d",p[l]); //画面出力
printf("\n");
}
}
}
return 0;
}
再帰呼び出しによる順列パターンの生成
先のプログラム例のfor文によるネストを再帰呼び出しによって実現した例です。下図に３個の数字から３個取り出す場合を例に順列生成の考え方を図示します。k番目の数字を格納する配列をp[k]として、k番目を再帰呼び出しによって実現し、その数字p[k]はループ処理によって順に決定していきます。
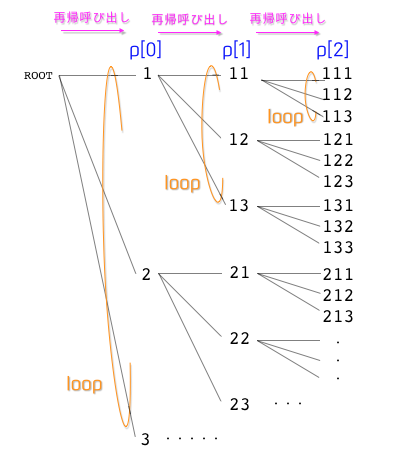
Fig.2 再帰呼び出しによる順列生成の考え方
例 perm_overlap.c
#include <stdio.h>
#define MAX 8 //１から最大８までの数字
void perm(int k); //プロトタイプ宣言
int p[MAX]; //順列[何番目の文字]
int n,r; //nPr
int main(void)
{
printf("異なるn個のものからr個を取ってできる順列nPrを求めます。\n");
do {
printf("n>> "); scanf("%d", &n);
printf("r>> "); scanf("%d", &r);
} while(n<0 || n>=MAX || n<r);
perm(0);
return 0;
}
/*
* 重複順列
* @k番目の数字
*/
void perm(int k)
{
int i;
if(k == r){ //最後の数字まで決定したら
for(i=0; i<r; i++) printf("%d ",p[i]); //表示
printf("\n");
return;
}
else {
for(i=1; i<=n; i++){ //数字 1,2,... ,n
p[k] = i; //数字の設定
perm(k+1); //隣の数字を決める
}
}
}
上記の再帰関数を使って３個の数字１、２、３から２つの数字を取り出す場合をトレースした結果を下図に示します。
重複をチェックして順列パターンを表示する
次に先のプログラムにおいて、重複がない時だけパターンを表示するよう、重複をチェックする機能を関数として追加します。例 perm_check.c
#include <stdio.h>
#define MAX 16 //１から最大16までの数字
void perm(int k); //プロトタイプ宣言
int p[MAX]; //順列[何番目の文字]
int n,r; //nPr
int main(void)
{
printf("異なるn個のものからr個を取ってできる順列nPrを求めます。\n");
do {
printf("n>> "); scanf("%d", &n);
printf("r>> "); scanf("%d", &r);
} while(n<0 || n>=MAX || n<r);
perm(0);
return 0;
}
/*
* 重複チェック
*/
int check(void)
{
int i,j;
for(i=0; i<r-1; i++){
for(j=i+1; j<r; j++)
if(p[j]==p[i]) return 0;
}
return 1;
}
/*
* 重複順列
* @k番目の数字
*/
void perm(int k)
{
int i;
if(k == r){ //最後の数字まで決定したら
if(check()){ //重複がなければ
for(i=0; i<r; i++) printf("%d ",p[i]); //表示
printf("\n");
}
return;
}
else {
for(i=1; i<=n; i++){ //数字 1,2,... ,n
p[k] = i; //数字の設定
perm(k+1); //隣の数字を決める
}
}
}
重複パターンは生成を打ち切る
先のプログラムでは、重複を含む数字のパターンを作成したのちチェックすることで、順列を表示しました。しかし、パターン数が増えると処理に対する負荷が大きくなり、結果を得るため時間がかかってきます。そこで、パターンの作成過程で、同じ数字が出てきた場合にはそのパターンの作成を中止し、次のパターンの生成に進むように改良します。各数字ごとに使用済みかそうでないかを示すためのフラグを配列をとして用意することにします。例 perm.c
#include <stdio.h>
#define MAX 16
void perm(int k);
int p[MAX]; //順列[何番目の文字]
int f[MAX]; //使用済数字フラグ[使用済数字] 0:未使用、1:使用済み
int n,r; //nPr
int main(void)
{
printf("異なるn個のものからr個を取ってできる順列nPrを求めます。\n");
do {
printf("n>> "); scanf("%d", &n);
printf("r>> "); scanf("%d", &r);
} while(n<0 || n>=MAX || n<r);
perm(0);
return 0;
}
/*
* nPr
* @k 番目の数字
*/
void perm(int k)
{
int i;
if(k == r){ //揃ったら
for(i=0; i<r; i++) printf("%d ",p[i]); //表示
printf("\n");
return;
}
else {
for(i=1; i<=n; i++){ //数字 1,2,... ,n
if(f[i]) continue; //使用済みなら次の数字を
p[k] = i; //数字の設定
f[i] = 1; //iを使用済み数字に
perm(k+1);
f[i] = 0; //使用済みを解除
}
}
}
組み合わせ
n個からr個取り出す組みわせの数は、次式で求めることができます。 $$ \ _{n}C_{r} $$ この式を含む組み合わせ数は次式のように書き表すこともできます。 $$ \ _{n}C_{r} = \ _{n-1}C_r + \ _{n-1}C_{r-1}$$ $$ r=0の時\ \ _{n}C_0 = 1 $$ 最初の項$\ _{n-1}C_r$は、特定の数字を選択した時の残りの$n-1$個の数字からr個を選択したときの組み合わせ数を表し、二つ目の項$\ _{n-1}C_{r-1}$は特定の数字を含めたとき、残り$n-1$個から$r-1$個の数字を選択したときの組み合わせ数と考えることができます。例えば、１から５の数字の中から3個取り出す組み合わせは、
-
[5,4,3],[5,4,2],[5,4,1],[5,3,2],[5,3,1],[5,2,1],
[4,3,2],[4,3,1],[4,2,1],
[3,2,1]
特定の数字として５を選択した場合について考えます。５を含まない残りの4,3,2,1の4つの数字から3つの数字を選択する組み合わせは、上記の組み合わせの2、3行目に相当する４パターンがあります。1つ目の数字を５として、残りの２つの数字を残りの数字4,3,2,1の中から２つ選択するパターンは上記の1行目の６パターンがあります。これで合計の組み合わせ数が１０になります。
以下はこの考え方に基づいて再帰呼び出しを使って実現したプログラム例です。
例 comb.c
#include <stdio.h>
#define MAX 16
void comb(int k, int n, int r);
int c[MAX];
int main(void)
{
int n,r;
printf("n個からr個を取り出す組み合わせのパターンを求めます\n");
do{
printf("n>> ");
scanf("%d",&n);
printf("r>> ");
scanf("%d",&r);
}while(n>=MAX || r>n);
comb(0,n,r);
return 0;
}
/*
* 組み合わせ
* nC0 = 1, nCr = n-1Cr + n-1Cr-1
*/
void comb(int k, int n, int r)
{
int i;
if(r==0){ //組み合わせ数は１
for(i=0; i<k; i++) printf("%d ",c[i]);
printf("\n");
}
else if(n==r){ //すべての数字
for(i=r; i>0; i--) c[k++]=i;
for(i=0; i<k; i++) printf("%d ",c[i]);
printf("\n");
}
else{
comb(k,n-1,r); //数字nを除く数字からr個取り出す組み合わせ
c[k] = n; //k番目に特定される数字n
comb(k+1,n-1,r-1); //数字nを含み、残りのn-1個からr-1個を取り出す組み合わせ
}
}
Nクィーン問題
８クィーン問題
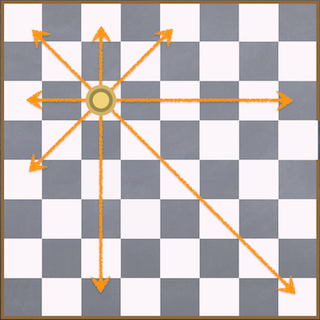８x８のマス目のあるチェス盤に８個のクィーンをどう配置したら互いに一手で取り合うことのないかを考える問題です。クィーンは縦横斜めのいずれかの方向に移動することができます。ただし、他のクイーンを飛び越えて移動することはできません。この問題を解く方法の一つは、８x８(=64)個のマス目に８個のクィーンを配置するすべてのパターンを調べてみることです。その組合せ数は
64C8 = 64 x 63 x ... x 2 x 1 = 4426165368 通
りあります。次に、１列もしくは１行にはクィーンは一つしか置けないことから、調べるべきパターン数は、
88 = 8 x 8 x ... x 8 x 8 = 16777216 通り
に減らすことができます。また、コードに置き換える場合も、２次元配列ではなく、r列のc行目への配置を１次元配列として、次のように取り扱うことができるようになります。
q[r] = c
equeen.c
#include <stdio.h> #include#define N 8 void printBoard(void); int check(void); void setQueen(void); int q[N]; //q[列]=行 /* * 盤面 */ void printBoard(void) { int i,j; for(i=0; i<N; i++) printf("%2d",i); printf("\n"); printf("-+----------------\n"); for(i=0; i<N; i++){ //行 printf("%d|",i); for(j=0; j<N; j++){ //列 q[j]==i ? printf(" Q") : printf(" ."); } printf("\n"); } printf("\n"); } /* * 縦横斜めチェック */ int check(void) { int i,j; for(i=1; i<N; i++){ for(j=0; j<i; j++){ //同一行 もしくは 斜線上 if(q[i]==q[j] || abs(q[i]-q[j])==abs(j-i)) return 0; } } return 1; } /* * クイーンの配置 * @row 配置される列 */ void setQueen(void) { int i,j,k,l,m,n,o,p; for(i=0; i<N; i++){ //行の移動 q[0] = i; //0列目への配置 for(j=0; j<N; j++){ q[1] = j; //1列目への配置 for(k=0; k<N; k++){ q[2] = k; for(l=0; l<N; l++){ q[3] = l; for(m=0; m<N; m++){ q[4] = m; for(n=0; n<N; n++){ q[5] = n; for(o=0; o<N; o++){ q[6] = o; for(p=0; p<N; p++){ q[7] = p; if(check()) printBoard(); } } } } } } } } } int main(void) { setQueen(); return 0; }
再帰による８クィーン問題の解決
先のプログラムでは、各列へのクィーンのすべての配置パターンを生成するためにforによる多重ループを利用しました。多重ループは再帰によって書き換えが可能です。演習１
次のプログラムは、先の８クィーンの配置パータンを求めるプログラムを再帰呼び出しを使って書き換えたものです。再帰関数setQueen()の空欄を埋めて完成させなさい。また、Nクィーンに対応できるように変更されたい。
equeen_rcv.c
#include <stdio.h>
#include <stdlib.h>
#define N 8
void printBoard(void);
int check(void);
void setQueen(int col);
int q[N]; //q[列]=行
/*
* 盤面
*/
void printBoard(void)
{
中略
}
/*
* 縦横斜めチェック
*/
int check(void)
{
中略
}
/*
* クイーンの配置
* @row 配置される列
*/
void setQueen(int col)
{
int i;
if([[空欄ア]]){ //配置終了
if([[空欄イ]]) printBoard();
}
else {
for(i=0; i<N; i++){ //行
q[col] = i; //配置
setQueen([[空欄エ]]); //次の列
}
}
}
int main(void)
{
setQueen(0);
return 0;
}
演習２ 配置パターンの数を表示するようプログラムを追加修正しなさい。
完成例
equeen_rcv.c
#include <stdio.h>
#include <stdlib.h>
#define N 8
void printBoard(void);
int check(void);
void setQueen(int col);
int q[N]; //q[列]=行
int count; //パターン数
/*
* 盤面
*/
void printBoard(void)
{
int i,j;
printf("No.%2d\n",count);
printf(" ");
for(i=0; i<N; i++) printf("%2d",i);
printf("\n");
printf("-+----------------\n");
for(i=0; i<N; i++){ //行
printf("%d|",i);
for(j=0; j<N; j++){ //列
q[j]==i ? printf(" Q") : printf(" .");
}
printf("\n");
}
printf("\n");
}
/*
* 縦横斜めチェック
*/
int check(void)
{
int i,j;
for(i=0; i<N-1; i++){
for(j=i+1; j<N; j++){
if(q[i]==q[j] || abs(q[i]-q[j])==abs(j-i))
return 0;
}
}
return 1;
}
/*
* クイーンの配置
* @col 配置される列
*/
void setQueen(int col)
{
int i;
if(col==N){ //配置終了
if(check()==1){
printBoard();
count++;
}
}
else {
for(i=0; i<N; i++){ //行の移動
q[col] = i; //配置
setQueen(col+1); //次の列
}
}
}
int main(void)
{
setQueen(0);
return 0;
}
バックトラック法
先のプログラムにおいて、Nの値を８ではなく９もしくは１０に変更して実行してみてください。８の時には気にならなかった処理速度のことが気になるはずです。下図に示すように、出発点から枝分かれしながら配置パターンを作り出し、N個のクィーンの配置が完了した時点でそれが解なのかどうかをチェックする方法には多くの無駄があります。実際には枝分かれした時点でこれ以上進んでも配置できないことが明らかになる場合もあるからです。この無駄を減らすために、先に進まず後戻りして別のパターンに進むことで解を見つける方法をバックトラック法と言います。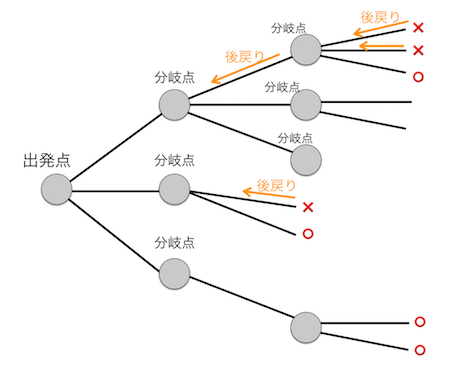
バックトラック法では、配置を完了する前に縦横斜めの配置が可能か判断する必要があります。
equeen_rcv.c
#include <stdio.h>
#include <stdlib.h>
#define N 8
void printBoard(void);
int check(void);
void setQueen(int row);
int q[N]; //q[列数]=行数
int flag1[N],flag2[2*N],flag3[2*N]; //配置済み,縦横、斜め右上、斜め左上
int count; //パターン数
/*
* Nクィーン問題（バックトラック）
*/
int main(void)
{
setQueen(0);
return 0;
}
/*
* 配置フラグ
* @row:行, col:列 state 0:clear, 1:block
*/
void setFlag(int row, int col, int state)
{
flag1[row]=state; //縦横
flag2[col+row]=state; //斜め右上
flag3[[[空欄ア]]]=state; //斜め左上
}
/*
* クイーンの配置
* @col 配置される列
*/
void setQueen(int col)
{
int i;
if(col==N){ //配置終了
printBoard();
count++;
}
else{
for(i=0; i<N; i++){ //行の移動
if(!flag1[i] && !flag2[col+i] && !flag3[col-i+N-1]){ //配置済み?
q[col] = i;
setFlag(i,col,1); //配置済み
setQueen([[空欄イ]]); //次の列
[[空欄ウ]]; //バックトラック:配置済み解除
}
}
}
}
/*
* 盤面表示
*/
void printBoard(void)
{
int i,j;
printf("No.%2d\n",count);
printf(" ");
for(i=0; i<N; i++) printf("%2d",i);
printf("\n");
printf("-+----------------\n");
for(i=0; i<N; i++){ //行
printf("%d|",i);
for(j=0; j<N; j++){ //列
q[j]==i ? printf(" Q") : printf(" .");
}
printf("\n");
}
printf("\n");
}
配置の可否のチェック
一つの列には一つのクィーンだけを配置するものとしているので列方向のチェックはしません。行方向のチェックについては、同じ行番号であるかをチェックするだけです。では斜め方向の判定はどうしたらよいでしょう。
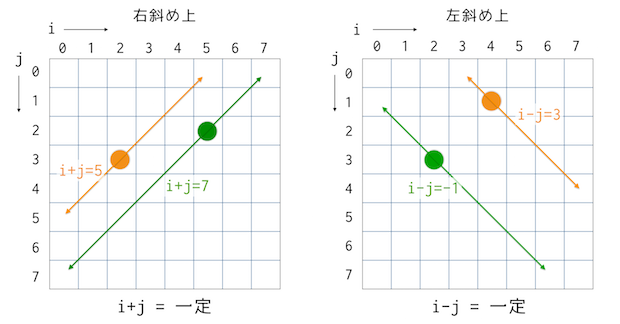
下図に示すように配置されたクィーンの右斜め上の位置は、列番号をi、行番号をjとするとi + jの値はどこでも一定となります。一方、左斜め上の位置ではi - jの値がどこでも一定となります。ただし、i<jの場合にはマイナスになるため、そのままでは配列の添え字には利用できません。そこで、実際にはマス目数を加えたi-j+Nの値が一定であるものとして利用します。
expand_lessBack to TOP
