内 容
線形探索
配列はデータが直線上に並んだ構造をしています。このようなデータの集まりから、目的のデータを先頭から順次探し出すことを線形探索(linear search)と言います。次は、整数型の配列の中から探したい値が何番目の要素に格納されているかを調べるプログラム例です。探索対象となる1次元配列aと探したい値keyを引数として線形探索を実現する関数lenear_searchを定義しています。
linear_search.c
#include <stdio.h>
#define N 7
/* 線形探索
* @ a[]: data
* @ key: search key
*/
int linear_search(int a[],int key)
{
int i=0;
for(i=0; i<N; i++){
if(a[i]!=key) continue; else break;
}
return i;
}
int main(void)
{
int a[N] = {5,3,8,7,1,9,2};
int key;
int n=0;
printf("探す数>> ");
scanf("%d",&key);
n = linear_search(a,key);
if(n<N)
printf("%d番目の要素に見つかりました。\n",n);
else
printf("見つかりませんでした。\n");
return 0;
}
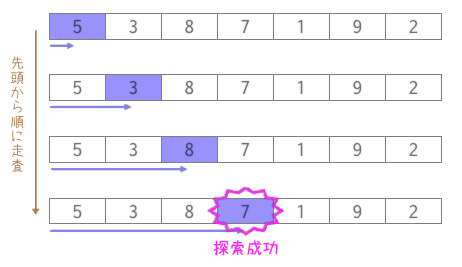
[アルゴリズム]
-
1. 配列DATAを先頭要素から走査するために、添字をi=0とする。
2. 要素DATA[i]が探索したい値KEYに等しいかを調べ、
2-1.等しければ探索処理を中止する。
2-2.等しくなければ探索の対象を一つ先に進めて(i++)処理を継続する。
3. 添字iの値が、データ数Nよりも
3-1. 小さければ、「探索成功」となる。
3-2. 同じならば、「探索失敗」となる。
キーとバリューと、データ構造
データを識別するために付与された情報をキー(key)、そのデータが持つ任意の情報をバリュー(Value)と言います。この2つからなるデータ構造は大変シンプルであることから、スケーラブル(規模の拡大に対応可能)なデータシステムの構築に利用されています。さらに、大量のデータの中からキーを使って高速なデータ探索をも可能にしています。線形探索の関数linear_searchでは、配列の要素をキー、その要素の添字がバリューとして取り扱われています。しかし、配列の要素とインデックスの関係はデータを並べ替えるといった処理によって変わってしまいます。探索対象とするデータは、このような変化にも対応できるようにキーとバリューが一つの塊となるようなデータ(構造体)として表現されるべきです。
二分探索
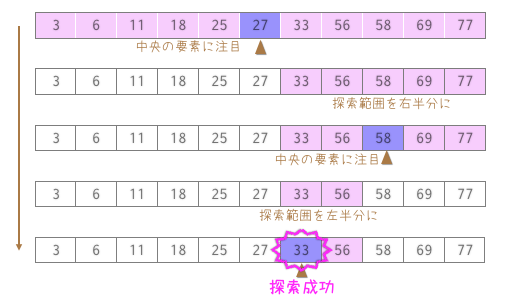
二分探索
探索の対象となるデータ列が、あらかじめ昇順もしくは降順にソート済みの場合に、高速に目的のデータを探索することができるアルゴリズムです。データ列があらかじめ昇順でソート済みだとします。データ列の中央の位置midの要素が、目的のデータならば探索を終了し、大きければ中央よりも右側のを探索範囲に、小さければ中央よりも左側を探索の範囲にします。さらに探索範囲を中央で左右に二分し、目的の値が見つかるまで探索を繰り返します。
binary_search.c
#include <stdio.h>
#define N 8
/*
* 二分探索
* @ *p: pointer to data
* @ n: size of elements
* @ key: search key
*/
int binary_search(int *p, int n,int key)
{
int left=0;
int mid;
int right=n-1;
int i=0;
while(i<n){ printf("%3d",*(p+i)); i++; } printf("\n");
while(left<=right){
mid = (left+right)/2;
if(*(p+mid)==key)
return mid;
else if(*(p+mid)>key)
right = mid-1;
else
left = mid+1;
}
return -1; //could not find;
}
int main(void)
{
int a[N] = {12,19,23,28,33,39,41,56};
int i=0,n,target;
while(i<N) printf("%5d",a[i++]);
printf("\n");
printf("探す値>> ");
scanf("%d",&target);
n = binary_search(a,N,target);
if(n<0)
printf("その整数はありません。\n");
else
printf("%d番目の要素に見つかりました。\n",n);
return 0;
}
内挿探索
内挿探索は二分探索のように単純に中央の位置を決めるのではなく、どの辺りに目的の値があるかをあらかじめ予測した上で調べる方法です。この点を除き、そのアルゴリズムは二分探索とほとんど変わりません。下図に示すソート済みの配列aを例に、予測の方法を考えます。

探索範囲の下限と上限のインデックスをそれぞれlower、upperとします。また、目的の値が位置すると予測されるインデックスをmidとします。探索範囲の下限と上限の値の差分\(a[upper] - a[lower]\)と下限の値a[lower]と目的の値dataとの差分の比が、対応するインデックスの差分の比に等しいとすると、次式が成り立ちます。
\[ data - a[lower] : a[upper] - a[lower] = mid - lower : upper - lower : \] この関係より、midは次式を使って求めることができます。 \[ mid = lower + \frac{data - a[lower]}{a[upper] - a[lower]} * (upper - lower)\] 上図の値をこの式に当てはまると、midの値として2が得られます。
interpolation_search.c
#include <stdio.h>
#define N 8
int interpolation_search(int *p, int n, int key)
{
int lower=0,upper=n-1,mid;
while(lower <= upper){
mid = lower + (((data-(p[lower]))*(upper-lower))/(p[upper]-p[lower]));
if(p[mid] == key){
return mid;
}
else {
if(p[mid] < key)
lower = mid + 1;
else
upper = mid - 1;
}
//printf("%d | %d | %d \n",lower,mid,upper);
}
return -1;
}
int main(void)
{
int a[N] = {12,19,23,28,33,39,41,56};
int data,index;
printf("目的の値> ");
scanf("%d",&data);
index = interpolation_search(a,N,data);
if(index<0)
printf("見つかりませんでした。\n");
else
printf("%d番目に見つかりました。\n",index);
return 0;
}
アルゴリズムと計算量
ある問題を解決するためのアルゴリズムが複数あった場合、どのアルゴリズムを選択すべきかを判断するための目安が必要です。目安にはアルゴリズムが計算に使う「時間」と「領域」(記憶容量)があり、それぞれを、時間計算量と、領域計算量と呼んでいます。いずれも、入力データの量によって決定される値です。ここでは時間計算量について説明していきます。オーダー
実際の計算時間は、利用するコンピュータのプロセッサやメモリ装置などの性能に左右されます。そのような違いは考えず、入力されるデータの量をパラメータとして計算量を考えます。データ量を\(n\)とした時のアルゴリズムの計算量\(f(n)\)は、プログラムの1ステップ当たりの計算回数を表す関数\(g(n)\)に対して2つの係数cと\(n_0\)が存在し、 \[f(n) \leqq cg(n), n \geqq n_0\] の関係が成り立つ時、\(f(n)\)は\(g(n)\)のオーダーと呼び、次式のように記述します。
\[f(n) = O(g(n))\] これをオーダー記法と言います。
関数\(g(n)\)は、データ量に比例して計算回数が増える場合は\(g(n)=n\)、2重ループによる処理の場合には計算回数は\(n×n\)回になるので、\(g(n)=n^2\)となります。二分探索のように探索範囲が半分に変化していくようなアルゴリズムでは、\(g(n)=\log_2 n\)となります。
次に、1ステップの処理時間を1nsecした場合のデータ量nに対するオーダーの変化を下表に示します。
| n | log n | n | n2 | n3 | 2n |
| 10 | 1nsec | 10nsec | 100nsec | 1μsec | 1μsec |
| 100 | 2nsec | 100nsec | 10μsec | 1msec | 40兆年 |
| 1000 | 3nsec | 1μsec | 1msec | 1sec | |
| 10000 | 4nsec | 10μsec | 0.1sec | 16分 | |
| 100000 | 5nsec | 100μsec | 10sec | 11日 | |
| 1000000 | 6nsec | 1sec | 0.1sec | 31年 | |
| 10000000 | 7nsec | 10sec | 0.1sec | 3000年 |
一つのプログラムの中には、1回で済む処理もあれば、同じ処理を何回も繰り返したり、2重ループによる処理など、複数のオーダが含まれます。それぞれ処理の計算回数を合計することでプログラム全体の計算回数を求めることはできます。しかし、この表からオーダーは、データ量nが大きくなると、より大きいオーダーに支配されることがわかります。大きなオーダーの項のみを考慮してその他の項を無視しても影響はありません。係数も無視することができます
オーダーの求め方
オーダーの求め方の手順を示します。- 各ステップの平均実行回数を求める。各種演算、関数呼び出し、判断、分岐をそれぞれ「1回の計算」とします。
- 入力データ数nに対する計算式を求める。
- 計算式中の最も増加率の大きい項のみ取り出す。
- 係数は無視する。
[計算例]
\[f(n) = 3n^2 + 5n + 7 = O(n^2) + O(n) + O(1) = O(max(n^2,n,1)) = O(n^2) \]
線形探索法と二分探索法のオーダー
線形探索法
線形探索法における計算量を求めてみましょう。次のコードのコメントに各行(ステップ)の平均実行回数とオーダーを示しています。
int linear_search(int *p, int n, int key){
int i=0; // 1回, O(1)
while(i<n){ // n/2回, O(n)
if(*(p+i) == key) // n/2回, O(n)
return i; // 1回, O(1)
i++; // n/2回, O(n)
}
return -1; // 1回, O(1)
}
二分探索法
二分探索法における計算量を求めてみましょう。二分探索では、探索の対象となる要素の範囲が1/2になっていくので、計算量nに対して実行回数はlog nとして求められます。
int binary_search(int *p, int n, int key){
int left = 0; //1回, O(1)
int mid; //1回, O(1)
int right = n-1; //1回, O(1)
while(left<=right){ //log n回, O(log n)
mid = (left+right)/2; //log n回, O(log n)
if(*(p+mid) == key) //log n回, O(log n)
return mid; //1回, O(1)
else if(*(p+mid) > key) //log n回, O(log n)
right = mid -1; //log n回, O(log n)
else
left = mid + 1; //log n回, O(log n)
}
return -1; //1回, O(1)
}
よって、オーダーは、 \[ f(n) = 5O(1) + 7O(\log n) = O(max(1,\log n)) = O(\log n) \] となります。
この結果から、データが1000倍になった場合の計算時間は、線形探索法ではデータ数に比例して1000倍になり、二分探索ではオーダー\(\log_2 n\) から10回増えるだけであることがわかります。
処理時間の計測
あなたの作ったプログラムの実機での処理時間は、プログラムの先頭と最後にclock()関数を埋め込んで、その時間差を求めること知ることができます。例 processing_time.c
#include <stdio.h>
#include <time.h>
int main(void)
{
clock_t start,end;
start = clock();
/* ここに計測対象の処理を記述する */
end = clock();
printf("time: ");
printf("%f sec.\n", (double)(end-start)/CLOCKS_PER_SEC);
return 0;
}