第４週　ソートアルゴリズ
INDEX

本日の目標

  • ソートのアルゴリズムを理解して、利用することができる。
  • 構造体を使って表されるデータをソートすることができる。

予習・復習

　以下のスライドを利用して、予習と復習をしよう。復習では、自分の理解度を確認するために、実際にプログラムを作成し、意図する結果が得られるか確認しよう。
  1. ソートアルゴリズム

本日の講義・演習予定

  1. 線形探索
  2. 二分探索
  3. 計算量
  4. 演習問題
  5. 提出課題
内　容
  1. ソート
  2. 単純選択ソート
  3. バブルソート
  4. 挿入ソート
  5. シェルソート
  6. マージソート
  7. クイックソート

ソート

　データの集合を大小関係によって並べ替えることをソートと言います。例えば、学生を表すためのデータには名前、学籍番号、身長、試験の点数などがあります。身長をキーとしてソートをすれば、「低い順」もしくは「高い順」に並べ替えることになります。名前をキーとしてソートするなら「アルファベット」順、もしくは「五十音順」に並べ替えることなります。対象となるもの（オブジェクト）が持つ属性（オブジェクトを特徴付ける要素）のうち注目する情報をキーとして、「小さい順に並べ替えるか」、「大きい順に並べ替えるか」の順があり、それぞれ以下のように名前が付けれています。
　昇順：小さい順に並べる
　降順：大きい順に位並べる

　ソートするための代表的なアルゴリズムには、
  1. 単純ソート
  2. 単純選択ソート
  3. バブルソート
  4. 挿入ソート
  5. シェルソート
  6. クイックソート
があります。いずれも、「選択」、「交換」、「挿入」の３つの操作を応用することで並べ替えを実現しています。ただし、「コンピュータは１度に２つの値を比較することしかできない」ことが前提となります。

単純ソート

　バラバラに散らばっている数を小さい順（昇順）に並べ替える最も簡単な方法の一つは、互いに比較し合い自分より相手が小さければ交換することです。
simpe_sort.c
#define <stdio.h>
#define N 10 

void print_array(int a[], int size);
void simple_sort(int a[], int size);

int main(void)
{
    int data[N] = {21,12,8,65,22,40,34,17,7,51};

    printf("before: ");
    print_array(data,N);

    simple_sort(data,N);

    printf("after : ");
    print_array(data,N);
 
    return 0;
}

/* 単純ソート */
void simple_sort(int a[], int  n)
{
    int i,j,tmp;

    for(i=0; i <size-1; i++){		// i番目の要素と
        for(j=i+1; j<size; j++){	// それ以外の未ソートの要素を
            if(a[i] > a[j]){		// 比較し、左側の要素が大きければ
	            tmp = a[i];			// 交換
	            a[i] = a[j];
	            a[j] = tmp
            }
        }
    }
}

手順（昇順）

  1. 未ソート範囲の先頭要素とそれ以外の未ソート範囲の先頭要素を選択する。
  2. 選択した要素同士を比較しそれ以外の未ソート範囲にある要素の方が大きければ交換する。
  3. 未ソート範囲の先頭を一つずらす（先頭要素を確定する）。
  4. 未ソート範囲の要素数が１になるまで（１）から（３）を繰り返す。

計算量

　データ数をnとした時の比較の回数は、 \[(n-1) + (n-2) + \cdots + 1 = n(n-1)/2 \] したがって、求める計算量（オーダー）は、 \[O(max(n^2,n))\\ = O(n^2) \] となります。


関数形式マクロ

　ソートにおいて値の交換処理は高い頻度で発生します。交換処理を関数として定義しておくこともできますが、より手軽な記述方法としてマクロ形式関数があります。
　関数形式マクロは、引数を取ることができ、あたかも関数のように利用することができます。次に示す形式でプリプロセッサ指令した処理（文字列）を、呼び出された位置で展開してプログラムに埋め込みます。ただし、関数のように引数による受け渡しが行われるわけではありません。
#define マクロ名(引数列) 処理

　次の例は、値を交換する関数形式マクロswapの例です。swapを呼び出した位置で、コメント文に書かれているように関数形式マクロで定義した文字列が展開されます。 
#include <stdio.h>
#define swap(a,b){ int tmp; tmp=a; a=b; b=tmp; }

int main(void)
{
	int x=3,y=7;
	
	swap(x,y);
	/* swap(x,y);以下のように展開される
	{ int tmp; tmp = x; x = y; y = tmp; };
	*/
	printf("%d %d\n",x,y);
	return 0;
}

　このようにマクロ形式関数は通常の関数よりも手軽に使えますが、プログラム中で展開された時の前後関係については十分に検討する必要があります。次の例のように副作用が生じることがあるからです。 
#include <stdio.h>
#define swap(a,b) { int tmp; tmp=a; a=b; b=tmp; }

int main(void)
{
	int x=3, y=7;
	
	if(x>y)
	    swap(x,y);
	    /* { int tmp; tmp=a; a=b; b=tmp; }; <--セミコロンでifが終了してしまう */
	else
	    printf("Without the need to swap.\n");
	    
   printf("%d %d\n",x,y);
	return 0;
}
　このような場合の対応策として、do while文が利用できます。
#define swap(type, a,b) do{ type tmp; tmp=a; a=b; b=tmp; }while(0)

（＊引数typeを使って、型を指定することもできます。）

　複数行からなるコードをマクロ形式関数として定義することの意味についても触れておきます。高い頻度で利用される「交換処理」をswap()という記号に置き換えることで、細部を省略してアルゴリズムの全体の構造を明確化することに役立ちます。

単純選択ソート

　単純選択ソートは、最小値（最大値）を探して先頭要素と交換する、残った中から最小値（最大値）を探してその先頭要素と交換する、という作業の繰り返しで並べ替えを実現するアルゴリズムです。
sort_simple_select

手 順（昇順）

  1. 未ソート範囲から最小値を探す。
  2. 未ソート範囲の先頭要素と最小値である要素とを交換する。
  3. 未ソート範囲の先頭を一つずらす（先頭要素を確定する）。
  4. 未ソート範囲の要素数が１になるまで（１）から（３）を繰り返す。

計算量

　データ数をnとした時の比較の回数は、 \[(n-1) + (n-2) + \cdots + 1 = n(n-1)/2 \] したがって、求める計算量（オーダー）は、 \[O(max(n^2,n))\\ = O(n^2) \] となります。

演習

　先の手順に基づいて、int型の１次元配列aとその要素数nを引数として、整数を昇順に並べ替える関数void select_sort(int a[], int n)を定義しなさい。また、定義した関数を利用して、以下の10個の整数
　21,12,8,65,22,40,34,17,7,51
が正しく昇順に並べ替えられることを実行、確認しなさい。

バブルソート

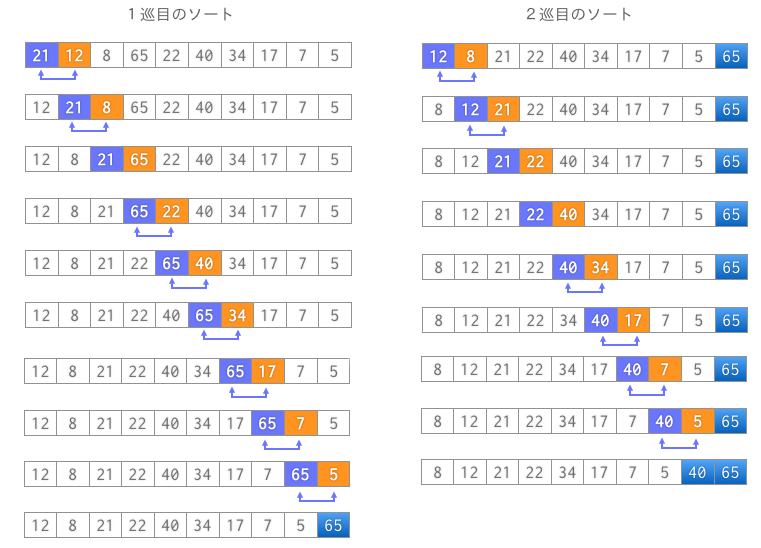
　隣り合う二つの要素を比較してソート順（昇順もしくは降順）と逆の場合には交換する、という作業を繰り返すことで一番大きな値が末尾に移動します。これを繰り返すことで、大きな値から順に後から確定していきます。あたかも水中の泡（バブル）が次々に上昇していくようなのでバブルソートという名前が付けられました。 sort_buble

手順[昇順]

  1. 未ソート部分の先頭要素と隣の要素を比較する。
  2. 先頭要素の方が大きければ、隣の要素と交換する。
  3. 比較する要素を一つずらす。
  4. （１）〜（３）を末尾手前まで繰り返し、未ソート部分の末尾の要素を確定する。
  5. （１）〜（４）をN−１回繰り返す。

計算量

　データ数をnとした時の比較の回数は、 \[(n-1) + (n-2) + \cdots + 2 + 1 = n(n-1)/2 \] したがって、求める計算量（オーダー）は、 \[O(max(n^2,n))\\ = O(n^2) \] となります。

演習

　先の手順に基づいて、int型の１次元配列aとその要素数nを引数として、整数を昇順に並べ替える関数void bubble_sort(int a[], int n)を定義しなさい。また、定義した関数を利用して、以下の10個の整数
　21,12,8,65,22,40,34,17,7,51
が正しく昇順に並べ替えられることを実行、確認しなさい。

挿入ソート

　n個の要素からなるリストを一度に並べ替えるのではなく、最初に先頭から２つの要素をソートの対象として並べ替え、次に先頭から３つの要素をソートするために３つ目の要素を適当な位置に挿入します。このように一つずつソートの範囲を広げて全体を並べ替えていく方法です。挿入位置は、すでにソートされている配列の中から探し出すことになるので、大きい方、または小さい方から順番に探していけば良く、いつもすべての要素と比較する必要はありません。
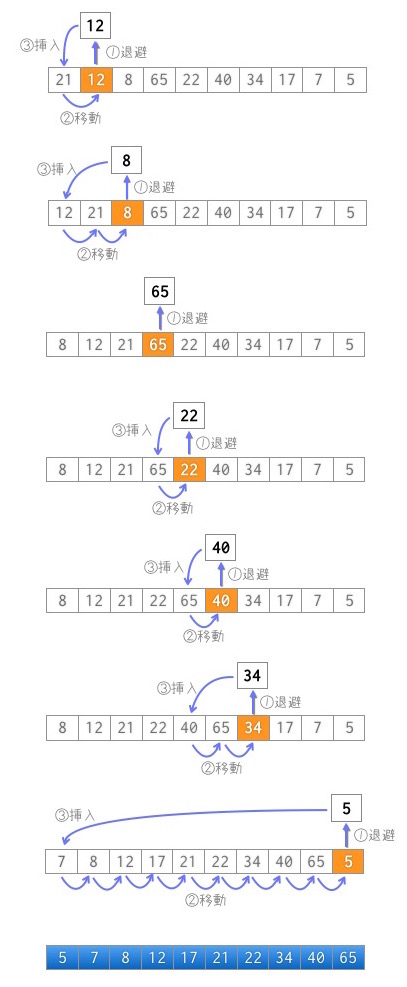
sort_insert

手順

　データ列\(a_0, a_1,a_2, , , a_n\)のうち、\(a_0, , , a_{i-1}\)までがソート済であるとします。また、tmpを退避用の変数とします。
  1. i番目のデータ\(a_i\)をtmpへ退避します。\((i\geqq 1)\)
  2. tmp(i番目のデータ\(a_i\))とそれより前方のソート済みのデータとを比較し、変数tmpより大きなデータ が見つかった場合は、それ以降のデータを一つずつ後方へずらして、tmpの値をその前に挿入します。
    1. i番目のデータの前方のデータを\(a_j、j=i-1\)として、前方のデータ\(a_j\)とtmpを比較する。
    2. 前方のデータが大きければ\(a_j > tmp\)、前方のデータを一つ後方へ移動、すなわち\(a_{j+1} = a_j\)とする。前方のデータが大きくなければ処理を終了して（３）へ進む。
    3. 比較の対象データを一つ前に進め\(j=j-1\)、手順ii.を繰り返す。ただし、j<0の場合には処理を終了して（３）へ進む。
  3. tmpの値をj+1の位置へ挿入する。すなわち、\(a_{j+1}=tmp\)とする。
  4. \(i=i+1\)としてソート範囲を一つ広げて、末尾\(i \lt n\)に到達するまで手順（１）〜（３）まで繰り返す。

計算量

　データの並びによって計算量が大きく影響を受けるアルゴリズムです。最悪の場合は、iのループにおけるjのループがi回行われる場合です。 \[ 1 + 2 + \cdots + n-1 \\ = n(n-1)/2 \\ = O(max(n^2, n))\\ = O(n^2) \]

演習

　先の手順に基づいて、int型の１次元配列aとその要素数nを引数として、整数を昇順に並べ替える関数void ins_sort(int a[], int n)を定義しなさい。また、定義した関数を利用して、以下の10個の整数
　21,12,8,65,22,40,34,17,7,51
が正しく昇順に並べ替えられることを実行、確認しなさい。
サンプルコードを見る
void ins_sort(int a[], int n)
{
    int i,j,tmp;

    for(i=1; i<n; i++){
        tmp = a[i];								// 退避
        for(j=i-1; j>=0 && a[j]>tmp; j--){ 		//前方のデータがtmpより大きい場合
            a[j+1] = a[j];						// 後方へ移動
        }
        a[j+1] = tmp;							// 挿入
    }
}


シェルソート

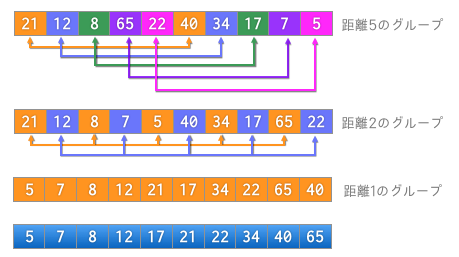
　挿入ソートの原理を応用したアルゴリズムです。挿入ソートでは先頭から連続したデータ列を対象としていましたが、シェルソートでは、対象となるデータを一定間隔離れたデータを１つのグループとして、その間隔を狭めながら並べ替えをするアルゴリズムです。 sort_shell

手順

  1. 間隔hを任意の値に設定する。（例では要素数N/2)
  2. 間隔hが１以上の間、（3）〜（５）を繰り返す。
  3. データ列を間隔hごとにグループ分けする
  4. 各グループごとに挿入ソート・アルゴリズムによって並べ替えをする。
  5. 間隔hの幅を狭める。（例ではh/2)

計算量

　データ数をn、グループ数をkとすると各グループのデータ数はn/kとなり、各グループごとのオーダーは\(O(n^2/k^2)\)として求められます。全体のオーダーはこれにkをかけた\(O(n^2/k)\)となるわけですが、グループ数kのとり方で値が大きく変化することがわかります。最良計算量が\(O(n)\)、最悪計算量が\(O(n \log n)\)で、 平均計算量が\(O(n^{1.25})\)と言われています。

演習

　先の手順に基づいて、int型の１次元配列aとその要素数nを引数として、整数を昇順に並べ替える関数void shell_sort(int a[], int n)を定義しなさい。また、定義した関数を利用して、以下の10個の整数
　21,12,8,65,22,40,34,17,7,51
が正しく昇順に並べ替えられることを実行、確認しなさい。
サンプルコードを見る
void shell_sort(int a[], int n)
{
    int i,j,k,h,x;

    for(h=n/2; h>0; h/=2){  			// 間隔を１になるまで半分に狭める
        for(k=0; k<h; k++){				// グループ数分繰り返す
            for(i=k+h; i<n; i+=h){		//以下挿入ソート
                x = a[i];
                for(j=i-h; j>=k && a[j]>x; j-=h)
                    a[j+h] = a[j];
                a[j+h] = x; 			//挿入
            }
        }
    }
}

マージソート

　マージソートは対象となるデータ列を繰り返し半分に分割していき、１つの要素になるまで繰り返し、分割したデータ列を昇順もしくは降順に並べ替えた一つのデータ列に併合(マージ）することを繰り返すことで並べ替えを実現するソートアルゴリズムです。

マージ

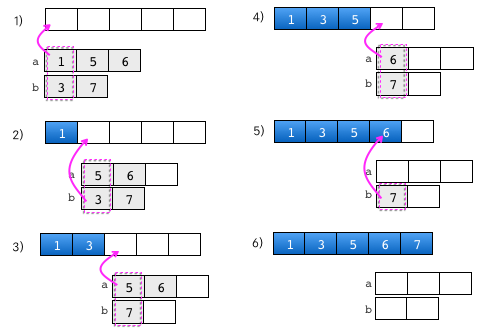
　複数のソート済みのリストを一つのリストにまとめることをマージ(merge)と言います。もちろん、マージ後のリストもまたソート済みとなっていなければなりません。次の例ではソート済みの配列aと配列bを配列cにマージしています。

merge

手順(昇順）

  1. マージする２つの配列とマージした結果を格納する配列の添字i,j,kをそれぞれ０とします。
  2. マージする配列の添字iとjの要素を比較し、一番小さい方の値をマージ先の配列にコピーします。
  3. 移動元の配列とマージ先の添字をそれぞれ＋１して、比較対象とマージ先を１つずらします。
  4. 比較対象する要素がなくなるまで、（２）〜（３）を繰り返します。
  5. マージする２つの配列のうち、まだ要素が残っている配列の要素をマージ先の配列にコピーします

演習

　先の手順に基づいて、マージする２つのint型の配列をa、b、その要素数をそれぞれna,nb、その結果を格納する配列をcを引数として、整数を昇順に並べ替える関数void merge(int a[], int na, int b[], int nb, int c)を定義しなさい。また、定義した関数を利用して、以下の10個の整数 　21,12,8,65,22,40,34,17,7,51 が正しく昇順に並べ替えられることを実行、確認しなさい。
サンプルコードを見る
#include <stdio.h>

void merge(int a[], int na, int b[], int nb, int c[])
{
    int i=0,j=0,k=0;

    while(i<na && j<nb)
        c[k++] = a[i]<b[j] ? a[i++] : b[j++];    //小さい方の値を格納

    while(i<na) c[k++] = a[i++];    //残った要素を格納
    while(j<nb) c[k++] = b[j++];
}

int main(void)
{
    int a[3] = {1,5,6};
    int b[2] = {3,7};
    int c[5];
    int i;

    merge(a,3,b,2,c);

    for(i=0; i<5; i++) printf("%d,",c[i]);
    printf("\n");

    return 0;
}

マージソート

　先のマージ操作を利用して並べ替えを実現するソートアルゴリズムです。その手順は大きく分けて、データ列を要素数が１になるまで２分割を繰り返すステップと、分割したデータ列を１つのデータ列になるまで繰り返すステップです。
merge_sort

手順

  1. n個の要素からなる配列をn/2個の要素からなる２つの部分配列に分割します。
  2. （１）の手順を要素数が１つになるまで繰り返します。
  3. 分割された部分配列をそれぞれソートします。
  4. ソート済みの部分配列をマージします。

計算量

　左図にように1回の分割やマージによってつくられたデータ列の集まりを階層と呼ぶことにします。２つのデータ列を一つのデータ列にマージするための比較回数は、例えば、互いに２つの要素から成るデータ列をマージする際の比較の回数は最大で3回、３つの要素なら5回、４つの要素なら７回になります。このことから一つの階層における計算量は全体の要素数にほぼ等しくなります。
　全体の要素数がn個の場合、一つのデータ列の要素が１個になるまでに分割(1/2)される回数kは、\(n(\frac{1}{2})^k = 1\)より、\(k = \log_2n\)となります。このことから、総計算量は \[O(n \log n)\] となることがわかります。

演習

　先の手順に基づいて、ソートの対象となる配列の左端のインデックスleftと右端のインデックスrightを引数として、昇順に並べ替える関数void merg_sort(int left, int right)を定義しなさい。ただし、ソートの対象となる配列aはグローバル変数として与えるものとします。また、定義した関数を利用して、以下の10個の整数 　21,12,8,65,22,40,34,17,7,51 が正しく昇順に並べ替えられることを実行、確認しなさい。
サンプルコードを見る
#include <stdio.h>
#include <stdlib.h>
#define N 10

//プロトタイプ宣言
void merging(int left,int mid,int right);
void merge_sort(int left, int right);
void print_array(void);

int a[N] = {21,12,8,65,22,40,34,17,7,5};
int work[N];  //作業用（マージ結果格納用）

void merging(int left,int mid,int right)
{
	int i,j,k;

	i=left;		//配列の左半分の先頭
	j=mid+1;	//配列の右半分の先頭
	k=left;	//マージ結果格納用配列のインデックス
	while(i<=mid && j<=right)
		work[k++] = a[i]<=a[j] ? a[i++] : a[j++];	//小さい方の値を格納

	while(i<=mid) work[k++] = a[i++];				//残った要素を格納
	while(j<=right) work[k++] = a[j++];
	
	for(i=left; i<=right; i++) a[i] = work[i];
}

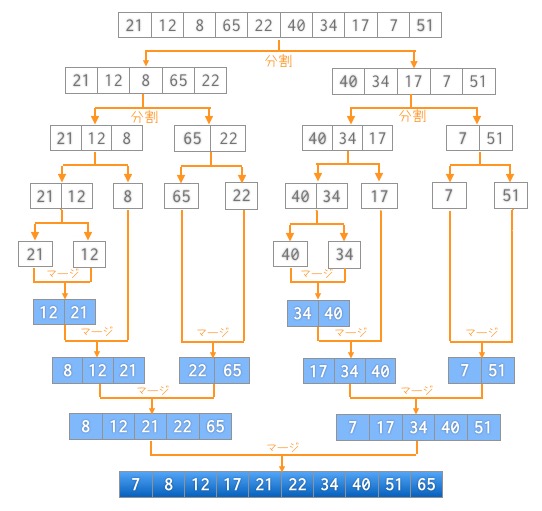
void merge_sort(int left, int right){
	int mid;

    if(left<right){
        mid = (left+right)/2;		//中央の位置を取得
        merge_sort(left,mid);		//左半分ソート（要素数が１になるまで再帰的に）
        merge_sort(mid+1,right);	//右半分ソート（要素数が１になるまで再帰的に）
		merging(left,mid,right);	//マージ
    }
}

int main(void)
{
	int i;

	printf("Before :");
	for(i=0; i<N; i++) printf(" %2d,",a[i]);
	printf("\n");

    merge_sort(0,N-1);

	printf("After  :");
	for(i=0; i<N; i++) printf(" %2d,",a[i]);
	printf("\n");

    return 0;
}

クイックソート

　並べ替え時間が最も高速なアルゴリズムの一つです。マージソートと同様にデータ列の要素が１つになるまで２分割を繰り返します。分割には枢軸(pivot)と呼ばれる適当な要素を設定し、これを基準として小さい値のグループと大きい値のグループに分けれられます。このためマージソートにあったマージの処理が不要となります。枢軸には、対象の配列の中央の要素や、右端、左端の要素などが選択されます。
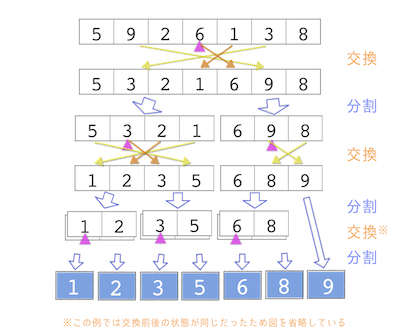
sort_quick

手順（昇順）

  1. 対象となる配列から任意の要素を選択します。この値を枢軸(pivot)と呼びます。
  2. 配列を枢軸よりも小さな値の部分配列と大きな値の部分配列に分割します。
    1. 配列の左右の添え字をそれぞれ、pl,prとします。
    2. 配列の左端要素から右に向かって、枢軸よりも大きな値が現れるまでplを走査します。
    3. 配列の右端要素から左に向かって、枢軸よりも小さな値が現れるまでpr走査します。
    4. 左側plが示す枢軸よりも大きいな値と、右側prが示す枢軸よりも小さな値を交換することで、枢軸よりも左側に小さな値を、右側に大きな値を集めます。ただし、pl>prになった場合は交換できません。
    5. pl<=prの間、さらに２）から４）を繰り返して配列を小さな部分配列を大きな部分配列に分割します。
  3. 分割した左右の部分配列にそれぞれ手順（１）〜（２）を、要素数が１になるまで再帰的に繰り返します。

計算量

　平均計算量は、 \[O(n \log n)\] となります。が、枢軸の取り方によっては最悪\(O(n^2)\)となります。

演習

　先の手順に基づいて、ソートの対象となる配列をa、その左端のインデックスleftと右端のインデックスrightを引数として、昇順に並べ替える関数void quick_sort(int a[], int left, int right)を定義しなさい。また、定義した関数を利用して、以下の10個の整数 　21,12,8,65,22,40,34,17,7,51 が正しく昇順に並べ替えられることを実行、確認しなさい。
サンプルコードを見る
void quick_sort(int a[], int left, int right)
{
    int pl,pr,pivot;

    if(left>=right) return; 		//交差していたら要素が１つだけと判断し終了
    pivot = a[(left + right)/2];	//配列の中央の要素を枢軸とする
    pl=left;						//小さい値グループ(左側)のインデックス
    pr=right;						//大きい値グループ(右側)のインデックス
    while(pl<=pr){
        while(a[pl] < pivot) pl++;	//右端Gから枢軸以上の値が現れるまで走査
        while(a[pr] > pivot) pr--;	//左端Gから枢軸以下の値が現れるまで走査
        if(pl<=pr){					//走査が交差していなければ
            swap(a[pl],a[pr]);		//左右の要素を入れ替える
            pl++;
            pr--;
        }
    }
    quick_sort(a,left,pr);		//左側グループを再帰的にソート
    quick_sort(a,pl,right);		//右側グループを再帰的にソート
}

expand_lessBack to TOP

expand_lessBack to TOP

演習問題

  1. １０個の整数 6,3,17,8,2,7,12,11,5,15を以下で定義したそれぞれの関数を利用して並べ替えなさい。引数には対象となる配列aとその要素数nを与えるものとします。
    1. 単純選択ソート法を使って、降順（大きい順）に並べ換える関数void select_sort_dec(int a[], int n)。
    2. バブルソート法を使って、昇順（小さい順）に並べ換える関数bouble_sort(int a[], int n)。ただし、先頭から末尾に向かって要素を確定すること。
    3. 挿入ソート法を使って、降順（大きい順）に並べ換える関数void ins_sort_dec(int a[], int n)。

  2. マージソートにおいて、マージの対象となる２つの配列の末尾にどの値よりも大きな値（番兵）を設定することで、関数mrgingで、比較できず残った要素を格納する処理を削除することができます。ただし、番兵を格納するために要素数を一つ余計に持つ配列を別途用意し、一旦その配列にデータをコピーする必要があります。番兵には適当な大きな値を設定します。（番兵として、int型の最大値を用いることが考えられます。その値はヘッダファイルlimits.hでINT_MAXとして定義されています。）

  3. 先のマージソートの例では、対象となる配列の全ての要素を別の作業用の配列に移動し、再び元の配列に戻すことでマージ処理を実現していました。このマージ処理を、始めに元の配列を２分割してその前半部分だけを作業用の配列に移動しておき、次に、その作業用の配列と元の配列の後半部分とを対象として、元の配列にマージすることで実現するプログラムを作成しなさい。

  4. 　学生の学籍番号と氏名、試験の得点からなるデータファイルachievement.data(データ数10件、CSV形式）を読み込んで、得点で降順にソートして結果を表示するプログラムを作成しなさい。データは以下に示す学生を表す構造体studentを使って取り扱うものとします。ソートのアルゴリズムにはどの方法を用いても良いものとします。
    5. struct student{
	int id;
	char name[32];
	int score;
}


OPEN ANSWER
  1. [解答例] 
    #include <stdio.h>
#define swap(a,b) { int tmp=a; a=b; b=tmp; }
#define N 10

void select_sort_dec(int a[], int n);
void bubble_sort(int a[], int n);
void ins_sort_dec(int a[], int n);
void print_array(int a[],int n);

int main(void)
{
	int a[] = {6,3,17,8,2,7,12,11,5,15};

	printf("Before: ");
	print_array(a,N);

	//select_sort_dec(a,N);	
	//bubble_sort(a,N);
	ins_sort_dec(a,N);

	printf("After : ");
	print_array(a,N);

	return 0;
}

/* 単純選択ソート(降順) */
void select_sort_dec(int a[], int n)
{
	int i,j;

	for(i=0; i<n-1; i++)
		for(j=i+1; j<n; j++)
			if(a[i]<a[j]) swap(a[i],a[j]);
}

/* バブルソート */
void bubble_sort(int a[], int n)
{
	int i,j;
	
	for(i=0;i<n-1; i++){
		for(j=n-1; j>i; j--)
			if(a[j-1]>a[j]) swap(a[j-1],a[j]);
		print_array(a,n);
	}
}

/* 挿入ソート（降順） */
void ins_sort_dec(int a[], int n)
{
	int tmp,i,j;

	for(i=1; i<n; i++){
		tmp = a[i];
		for(j=i-1; j>=0 && a[j]<tmp; j--)
			a[j+1] = a[j];
		a[j+1] = tmp;
	}
}

void print_array(int a[],int n)
{
	int i;

	for(i=0; i<n; i++)
		printf("%d ",a[i]);
	printf("\n");
}

  2. [解答例]
    3. #include <stdio.h>
#include <limits.h>
#define N 10

void print_array(int a[], int n);

int a[N] = {21,12,8,65,22,40,34,17,7,5};
int al[N],ar[N];

void merging(int left, int mid, int right)
{
	int i,j=0,k=0;

	for(i=left; i<=mid; i++) al[j++] = a[i];	
	al[j] = INT_MAX;	//番兵
	print_array(al,j);
	for(i=mid+1; i<=right; i++) ar[k++] = a[i];	
	ar[k] = INT_MAX;	//番兵
	print_array(ar,k);

	for(i=left,j=0,k=0; i<=right; i++)
		a[i] = al[j] <ar[k] ? al[j++] : ar[k++];
}

void merge_sort(int left, int right)
{
	int mid;

	if(left < right){
		mid = (left + right)/2;
		merge_sort(left,mid);
		merge_sort(mid+1,right);
		merging(left,mid,right);
	}
}

void print_array(int a[], int n)
{
	int i;
	for(i=0; i<n; i++)
		printf("%d ",a[i]);
	printf("\n");
}

int main(void)
{
	printf("Before: ");
	print_array(a,N);

	merge_sort(0,N-1);

	printf("After : ");
	print_array(a,N);
	
	return 0;
}

  3. [解答例] 
    #include <stdio.h>
#include <stdlib.h>
#define N 10

//プロトタイプ宣言
void merging(int a[], int left,int mid,int right);
void _merge_sort(int a[], int left, int right);
int merge_sort(int a[], int n);
void print_array(int a[], int n);

int *work;  //作業用領域

void merging(int a[], int left,int mid,int right)
{
	int i,wi,j=0;
	int k=left;

    for(i=left,wi=0; i<=mid; i++,wi++) work[wi] = a[i];	//左半分のみコピー

	//左半分workと右半分aを比較して、小さい方をaの先頭から格納する
    while(i<=right && j<wi)
        a[k++] = work[j]<=a[i] ? work[j++] : a[i++];

	//workに残っている要素があればaに移す
    while(j<wi) a[k++] = work[j++];
}

void _merge_sort(int a[], int left, int right)
{
    int mid;

    if(left<right){
        mid = (left+right)/2;	//中央の位置を取得
        _merge_sort(a,left,mid);	//左半分ソート
        _merge_sort(a,mid+1,right);	//右半分ソート
		printf("--> %d %d %d\n",left,mid,right);
		merging(a,left,mid,right);	//マージ
    }
}

int merge_sort(int a[], int n)
{
	//作業用領域確保
	if((work = calloc(n,sizeof(int))) == NULL) return -1;

    _merge_sort(a,0,n-1);	//マージソート呼び出し

    free(work);	//作業用領域解放

    return 0;
}

void print_array(int a[], int n)
{
	int i;

	printf("[");
	for(i=0; i<n; i++) printf(" %2d,",a[i]);
	printf("]\n");
}

int main(void)
{
    int a[N] = {21,12,8,65,22,40,34,17,7,5};
    int i;

	printf("Before ");
	print_array(a,N);

    merge_sort(a,N);

	printf("After  ");
	print_array(a,N);

    return 0;
}

  4. [解答例] 
    #include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 10     //データ数

struct student_s {
    int id;
    char name[32];
    int score;
};
typedef struct student_s Student;

void swap_student(Student *p, Student *q);
void simple_sort(Student *);

void simple_sort(Student *sp)
{
    int i,j,max;
   
    for(i=0; i<N-1; i++){
        max = i;
        for(j=i+1; j<N; j++){
            if((sp+j)->score > (sp+max)->score)
                max = j;
        }
        swap_student(sp+i, sp+max);
    }
}

void swap_student(Student *p, Student *q)
{
    int tmp;
    char tmpc[32];

    tmp = p->id;
    p->id = q->id;
    q->id = tmp;

    strcpy(tmpc,p->name);
    strcpy(p->name,q->name);
    strcpy(q->name,tmpc);

    tmp = p->score;
    p->score = q->score;
    q->score = tmp;
}

int main(void)
{
    FILE *fp;
    char filename[32] = "achievement.data";
    Student *sp;
    int i,j;

    sp = (Student *)malloc(sizeof(Student)*N);

    if((fp=fopen(filename,"r"))==NULL){
        fprintf(stderr,"Can't open %s.\n",filename);
        return EXIT_FAILURE;
    }

    printf("------ READ DATA ------\n");
    for(i=0; i<N; i++){ 
        fscanf(fp,"%d,%[^,],%d",&(sp+i)->id,(sp+i)->name,&(sp+i)->score);
        printf("%d %s %d\n",(sp+i)->id,(sp+i)->name,(sp+i)->score);
    }
    fclose(fp);

    simple_sort(sp);    

    printf("------ RESULT ------\n");
    for(i=0; i<N; i++){ 
        printf("%d %s %d\n",(sp+i)->id,(sp+i)->name,(sp+i)->score);
    }
    free(sp);

    return 0;
}

expand_lessBack to TOP

今週の確認テスト テスト(PDF)

本日の提出課題

　与えられた整数の配列データを挿入ソートを使って昇順に整列し、次に、キーボードから入力した整数をそのソート済みデータの整列を崩さない適切な位置に挿入するプログラムkdai4-4.cを完成させなさい。挿入ソートは関数ins_sort()を定義して利用すること。新規データの挿入には挿入ソートと同じアルゴリズムを利用して関数ins_data()を定義して利用すること。対象となるデータは配列に初期値として与えるが、配列の要素数は後でデータを追加することを考慮し１０個として宣言している。
[ソースコード kadai4-4.c] 
#include <stdio.h>

/*
  挿入ソート(昇順)
	a[]: 配列データ, n:データ数
 */
void ins_sort(int a[], int n)
{
  // ここを埋める	
}

/*
  ソート済みデータへのデータの追加
	a[]: 配列データ, n:データ数, x: 追加データ
 */
void ins_data(int a[], int n, int x)
{
  //ここを埋める
}

/* 配列データの表示 */
void print_array(int a[], int n)
{
  //ここを埋める
}

int main(void)
{
	int data[10] = {19,7,34,78,40,65,21,83,51};
	int a;

	ins_sort(data,9);
	printf("ソート済み:\n");
	print_array(data,9);

	printf("\n追加データ> ");
	scanf_s("%d",&a);
	ins_data(data,10,a);
	print_array(data,10);		//結果表示

	return 0;
}

[実行例]
ソート済み:
7 19 21 34 40 51 65 78 83 
追加データ> 68
7 19 21 34 40 51 65 68 78 83


  • [提出方法]
    • 電子メールの添付ファイルとして提出してください。宛先は指定のアドレスです。
    • 表題は、課題４とします。
    • メール本文には、提出したプログラムの関数ins_sort()の（最悪）時間計算量とそのオーダーを記すこと。また、挿入ソートは対象となるデータの並びが計算量に大きく影響するアルゴリズムですが、なぜ、ある程度整列されたデータに対しては高速に動作するのかを説明しなさい。
    • 添付ファイルは下記の２点です。
      • 1) ソースコード・ファイル kadai4-4.c
      2) 実行結果画面(ウインドウのみ)のハードコピーの画像ファイル kadai4-4.jpg

  • [実行結果画面のハードコピーの取り方]
    1. [メニュー]→[アクセサリ]→Snipping Toolを起動する。ただし、Snipping Toolのウインドウが実行画面に重ならないように、必要に応じてウインドウを移動すること。
    2. タイトルバーを含めた実行結果画面をマウスドラッグして選択して、キャプチャする。
    3. メニューから「ファイル」→「名前をつけて保存」を選択する。ファイルの種類にはJPG形式を選択して、保存先フォルダを選び、ファイル名を付けて「保存」する。

  • [評価について]
    • プログラムの内容の評価とは別に以下の要件を満たすことを評価の前提とする。
    1. ソースコードがC言語で記述されていること。
    2. 提出されたソースコードファイルをコンパイルし、ワーニングやエラーが出力されないこと。
    3. 提出されたソースコードファイルから生成される実行形式ファイルを実行した結果、所定の出力結果が得られること。
    4. 提出されたソースコードは、インデントや適当な改行が施された見やすい状態であること。
    5. 変数の利用目的、処理や判定の意味など必要と思われる解説を簡潔にコメント文として付けること。
    6. 提出された実行結果の画面コピーは、コマンドプロンプトのウインドウのみとすること。

  • [提出期限]
    • 2019年 １２月１８日（水）午後２時まで