内 容
木構造
木構造
木構造
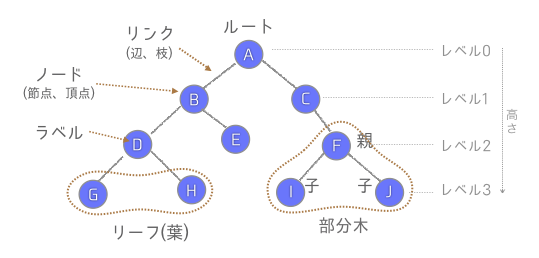
木構造とは、データを格納したノード(node/節)と、ノードとノードを連結するリンク(edge/枝)から構成されます。全体はルート(root/根)を頂点として、植物の木の枝が下向きに広がっていくように構成されます。あるノードに注目した時、そのノードの直下にリンクしたノードを子(child)と呼び、子の直上のノードを親(parent)と呼びます。親は子を複数持つことができますが、子は親を一つしか持つことができません。子を持たないノードをリーフ(leaf/葉)と呼びます。ルートの位置をレベル0として、その子の高さをレベル1、孫の高さをレベル2のように子孫の高さをレベルとして表します。
n分木
一つのノードに最大n個の子ノードを連結できる木構造をn分木と言います。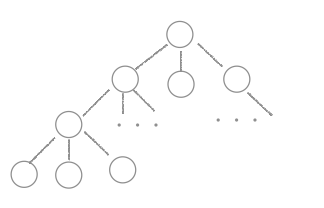
2分木
一つのノードに最大2個の子ノードを連結できる木構造を2分木と言います。すべてのノードが2個の子ノードを持つことですべてのレベルが満たされる場合を完全2分木、すべてのノードが2個の子ノードを持つが一部のレベルが欠けている場合を全2分木。また。すべてのノードが1個の子ノードしか持たない場合を最小二分木と言います。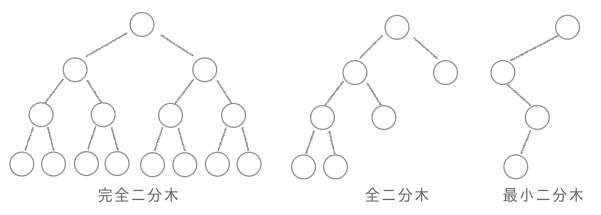
二分木の巡回方法
二分木を使って探索する方法には、幅優先探索と深さ優先探索があります。また、深さ優先探索においては、「行きがけ」、「通りがけ」、「帰りがけ」と呼ばれる3つの特別な巡回の方法があります。行きがけ、通りがけ、帰りがけ
ノードを巡る方法には、ノードの左側を通る際に訪問する「行きがけ」、ノードの下側を通る際に訪問する「通りがけ」、ノードの右側を通る際に訪問していく「帰りがけ」の3つの場合があります。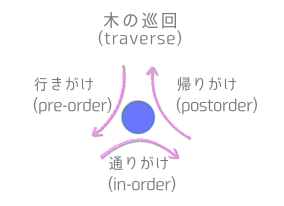
- 行きがけ(pre-order)
- ノードに立ち寄る -> 左部分木をなぞる -> 右部分木をなぞる
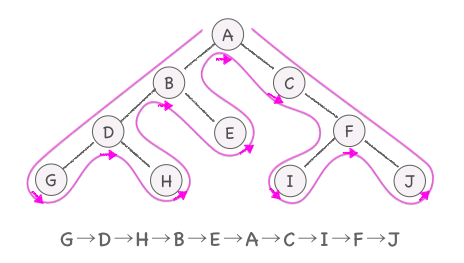
- 通りがけ(in-order)
- 左部分木をなぞる -> ノードに立ち寄る -> 右部分木をなぞる
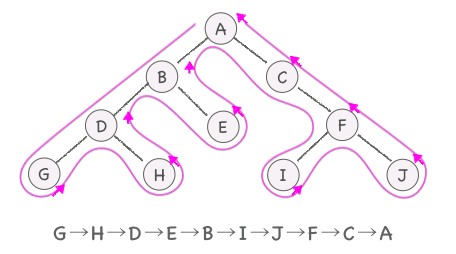
- 帰りがけ(postorder)
- 左部分木をなぞる -> 右部分木をなぞる -> ノードに立ち寄る
幅優先探索
あるノードを出発点として、同一レベルの隣接する左側のノードから右側に辿っていきます。それが終わると、次に高いレベルへと移って先と同様に左から右を辿っていく方法を幅優先探索と言います。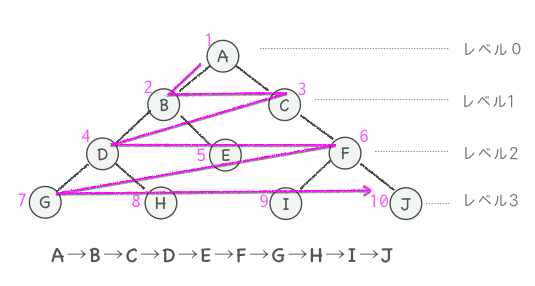
深さ優先探索
あるノードを出発点として、リンクで連結された子ノードを辿っていきます。リーフまで到達したら、親ノードに戻り反対側の連結された子ノードを辿っていく方法を深さ優先探索と言います。「行きがけ」、「通りがけ」、「帰りがけ」はそれぞれ深さ優先探索の方法の一つになります。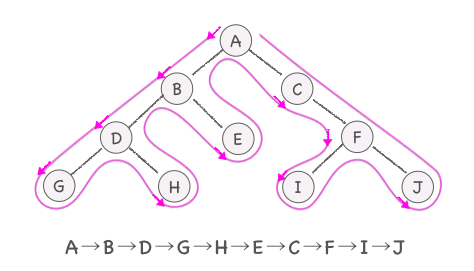
二分探索木
二分探索木
二分木を構成する各ノードは探索のためのキーを持つものとします。このとき、すべてのノードのキーが下図のように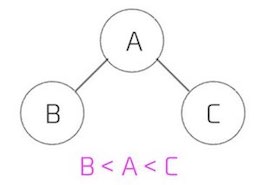
・右部分木のノードのキーは、そのノードのキーより大きい。
の条件を満たす二分木を二分探索木と言います。
プログラム例
binary_tree.c
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *left;
struct node *right;
};
typedef struct node Node;
void insert(int data);
Node *search(int key);
void preorder_traversal(Node *root);
void inorder_traversal(Node *root);
void postorder_traversal(Node *root);
Node *root = NULL;
/* データの追加 */
void insert(int data)
{
Node *new = (Node *)malloc(sizeof(Node)); //新ノード生成
Node *current,*parent;
new->data = data; //新ノードのメンバーへデータ設定
new->left = NULL;
new->right = NULL;
if(root==NULL){ //ルートが空ならば
root = new;
}
else{
current = root; //ルートからスタート
parent = NULL;
while(1){
parent = current; //親を設定
//左の枝へ追加(小さい値)
if(data < parent->data){
current = current->left; //左ノードへ移動
if(current == NULL){
parent->left = new; //左ノードが空なら新規ノード追加
return ;
}
}
//右の枝へ追加(大きい値)
else{
current = current->right; //右ノードへ移動
if(current == NULL){
parent->right = new; //右ノードが空なら新規ノード追加
return ;
}
}
}
}
}
/* 探索 */
Node *search(int key)
{
Node *current = root; //ルートからスタート
printf("Visiting: ");
while(current->data != key){
if(current != NULL) printf("%d -> ", current->data);
//左側探索
if(current->data > key)
current = current->left;
//右側探索
else
current = current->right;
//探索失敗(
if(current == NULL) return NULL;
}
return current;
}
/* 巡回(行きがけ) */
void preorder_traversal(Node *root)
{
if(root != NULL){
printf("%d ",root->data);
pre_order_traversal(root->left);
pre_order_traversal(root->right);
}
}
/* 巡回(通りがけ) */
void inorder_traversal(Node *root)
{
/***
ここを埋めて完成させる
***/
}
/* 巡回(帰りがけ) */
void postorder_traversal(Node *root)
{
/***
ここを埋めて完成させる
***/
}
空欄の回答
/* 巡回(通りがけ) */
if(root != NULL){
inorder_traversal(root->left);
printf("%d ",root->data);
inorder_traversal(root->right);
}
/* 巡回(帰りがけ) */
if(root != NULL){
post_order_traversal(root->left);
post_order_traversal(root->right);
printf("%d ",root->data);
}
計算量
ノード数をn、木の高さをhとすると、完全2分木における関係は \[n = 1 + 2^1 + 2^2 + \dots + 2^{n-1} = 2^h - 1\] と表すことができます。もし、探索対象のノードが一番下に位置した場合、その比較回数はhとなります。したがって \[h = \log_2 (n+1)\] となることから、オーダーは \[O(\log n)\] となります。また、最小二分木の場合には、n = hとなることから、オーダーは\(O(n)\)となります。演習
- 上記の二分探索木を使った探索プログラム例binary_tree.cにおいて、関数preorder_traversal()、inordertraversal()、postorder_traversal()がそれぞれ、2分木を正しく「行きがけ」、「通りがけ」、「帰りがけ」で巡回することをmain関数を追加して確認しなさい。
- 上記のプログラム例binary_tree.cにおいて、二分探索木での探索の手順について関数search()を使って、確認しなさい。
ヒープ
親ノードが常に子ノードより大きく(もしくは小さく)ならない二分木をヒープと言います。ヒープ
親ノードが常に子ノードより大きく(もしくは小さく)ならないように配置された場合、ルートには必ず木を構成するすべてのノードのうち一番小さな値(もしくは一番大きな値)が配置されることになります。ノードは左側から埋めていき、穴がないように配置されます。親ノードは必ず2つの子ノードを持ちますが、最後のノードだけは左側の子だけの場合もあります。ヒープは、下図のように配列を使って表すことができます。
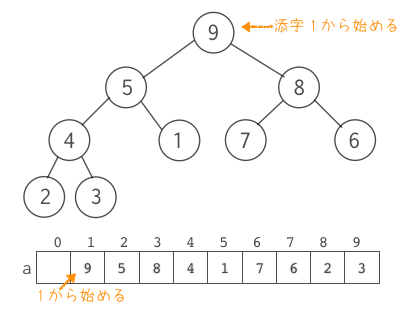
添字は1から始めることにして、先頭要素は使わないことにします。ルートの添字を1として、高いレベルになると添字が大きくなります。同じレベルでは左ノードから右に向かって添字が大きくなります。このようにノードを配置すると、i番目の要素a[i]の左右の子ノードをそれぞれa[i*2]、a[i*2+1]として、親ノードをa[i/2]として扱うことができます。
ヒープ化
ランダムに配置されたデータ列をヒープに構成する方法を考えます。ヒープは親と子の関係において大小関係が成り立つ構成である必要があります。ですから、子を持つ親ノードに注目して、子が親よりも大きい(もしくは小さい)場合にノードを入れ替えるようにします。子を持つ親ノードは、ヒープサイズをnとするとn/2で得ることができます。下図の例では、ヒープサイズが9なので、注目する親ノードの添字はi=9/2=4となります。i=4を親ノードとする部分木においては、子ノードの方が親ノードよりも大きいのでノードを交換します。左側の子ノードの方が右側の子ノードよりも大きいので、交換の対象は左側の子ノードとなります。次に添字iを1つ減じて、i=3を親ノードとする部分木に移動します。ここでも子ノードの方が親ノードよりも大きいのでノードを交換します。これを繰り返すことで残りの部分木ごとのヒープを実現していきます。ただし、下図のi=1の場合では、親ノードと子ノードを交換すると子ノードと孫ノードのヒープ関係が崩れてしまうため、子ノードに移動して孫ノードとの交換処理が必要になります。もし、次世代のヒープ関係が適切でなければ、ひ孫ノード、玄孫ノードというように子のないノード(リーフ)まで処理を継続しなければなりません。このような場合は再帰的に処理することで簡単に対応することができます。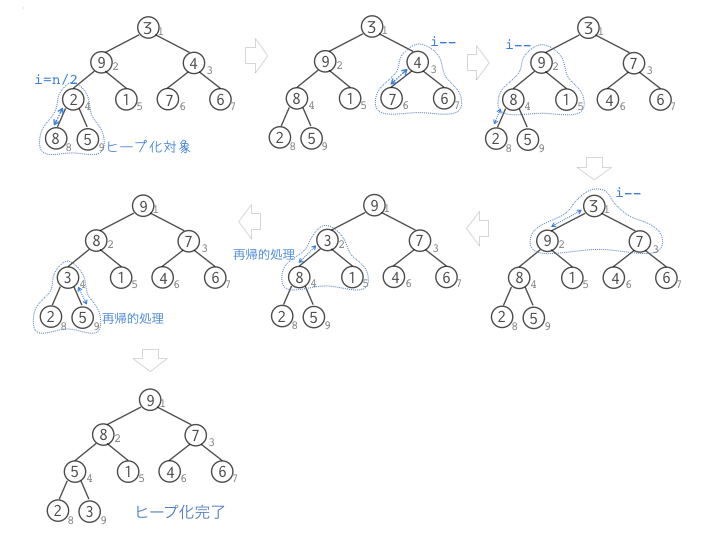
ノードの追加
新規のノードはヒープの最後、すなわち配列の末尾に追加されます。新しいノードの追加によってヒープはヒープではなくなる可能性があります。再びヒープに復元するための操作をシフトアップshift upと呼びます。親子の関係が親>子(もしくは親<子)の関係になっているかを調べて、そうでなければデータを交換していきます。追加したノードが適切な位置に移動するまで、上方にずらしていく処理ということになります。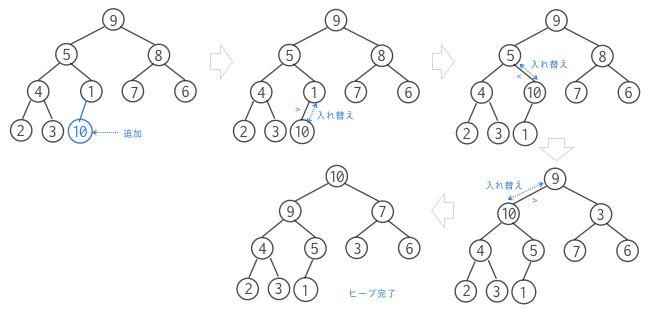
ノードの削除
ヒープからのルートの削除を考えます。ヒープからルートを削除する場合は、空いたルートに最後のノードを移動して埋めます。するとヒープが崩れてしまう可能性があります。再びヒープを復元するための操作をすることになります。親>子(もしくは親<子)の関係が成立するまで、ルートに移動したノードを下にずらす操作をheap_downもしくはshift_downと呼びます。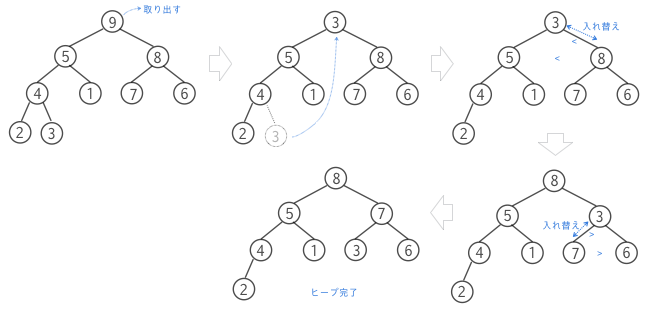
[プログラム例]
heap.c
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define swap(x,y) { int tmp=x; x=y; y=tmp; }
#define MAX 32
void ins_node(int value);
void del_node(void);
void build_heap(void);
void heapify_max(int i);
void heapify_min(int i);
void shift_up(int index);
void heap_down(int index);
int is_empty(void);
void print_tree(void);
//int a[MAX] = {0};
int a[MAX] = {0,21,12,8,65,22,40,34,17,7,0,};
int heapsize=9;
/* 乱数によるデータ生成 */
void init_data(int n)
{
int i;
if(n>=MAX){
printf("N is over max number.\n");
exit(EXIT_FAILURE);
}
srand((unsigned)time(NULL));
for(i=1; i<n; i++)
a[i] = rand()%50+2;
}
/* ヒープ化 */
void build_heap(void)
{
int i = heapsize/2; //右下端部分木からスタート
while(i>0)
heapify_min(i--); //ルートまで繰り返す
}
/* ヒープ化(rootへ最小値を) */
void heapify_min(int i)
{
int smallest = i; //親
int left = smallest; //左の子
int right = smallest; //右の子
if(a[i*2]) left = i*2;
if(a[i*2+1]) right = i*2+1;
if(left <= heapsize && a[left] <a[i]) smallest = left; //左子>親?
if(right <= heapsize && a[right] < a[smallest]) smallest = right; //右子>(左、親)
if(smallest != i){ //最大が親でなければ交換
swap(a[i],a[smallest]);
heapify_min(smallest);
}
}
/* ノードの追加(右下端) */
void ins_node(int value)
{
if(heapsize>MAX){
printf("Error: Heap array is overflow.\n");
exit(EXIT_FAILURE);
}
else {
heapsize++;
a[heapsize]=value; //右下端に追加
shift_up(heapsize); //再ヒープ(シフトアップ)
}
}
/* シフトアップ
ノード追加による
右下端から上に向かってヒープ(ルート最小) */
void shift_up(int i)
{
int parent,tmp;
if(i != 0){
parent = i/2; //親
if(a[parent] > a[i]){ //親の方が大きければ
swap(a[parent],a[i]); //交換
shift_up(parent); //再帰的にヒープ
}
}
}
/* ノードの削除(root) */
void del_node(void)
{
if(is_empty())
{
printf("Heap is empty.\n");
exit(EXIT_FAILURE);
}
a[1] = a[heapsize];
heapsize--;
if(heapsize>0) heap_down(1);
}
/* ヒープダウン
ノード削除による
ルートから下に向かってヒープ(ルート最小) */
void heap_down(int i)
{
int smallest; //左右の子の小さい方の添字
int left = i*2; //left child index
int right = left+1; //right child index
if(right>heapsize){ //右に子が無い
if(left>heapsize) //左右に子が無い
return;
else
smallest = left; //左側の子しか無い場合
}
else {
if(a[left]<=a[right]) //左右の子のうち小さい方は
smallest = left;
else
smallest = right;
}
if(a[i] > a[smallest]){ //子の方が小さければ
swap(a[i],a[smallest]);
heap_down(smallest); //下に移動
}
}
/* 木構造の表示 */
void print_tree(void)
{
int i,j,k;
int count=1,height,ns,smax;
int sidespace,space;
height = (int)(log(heapsize)/log(2))+1; //木の高さ
for(i=0; i<height; i++){ //レベル
sidespace = pow(2,height-i-1)-1;
for(k=0; k<sidespace; k++) printf(" "); //左側空白
space = pow(2,height-i)-1;
ns = pow(2,i);
for(j=0; j<ns && count<=heapsize; j++){ //レベルの最大数
printf("%2d",a[count++]);
for(k=0; k<space && j+1<ns; k++)
if(j%2) printf(" "); else printf("--"); //空白
}
printf("\n");
}
printf("\n");
}
/* 空か? */
int is_empty(void)
{
return !heapsize;
}
int main(void)
{
printf("[Before]\n");
print_tree();
printf("[Heap(min)]\n");
build_heap();
print_tree();
printf("[Delete Node]\n");
del_node();
print_tree();
printf("[Insert Node(10)]\n");
ins_node(10);
print_tree();
return 0;
}
注意:上記のソースコードには、未定義関数が含まれています。
ヒープ・ソート
ヒープ・ソート
ヒープサイズをn、ヒープを格納する配列aの先頭要素a[0]は使用しないものとして、ルートノードはa[1]に格納するものとします。ヒープソート(降順)の手順は、以下のようになります。ただし、あらかじめヒープ化されているデータ列を対象とします。もし、ヒープとなっていなければ事前にヒープ化しておかなければなりません。- ルートノード(最小値)を取り出す。
- ヒープの一番下の右端のノードをルート位置に移動する。(配列のa[1]と末尾要素a[n]とを交換する)
- ルートノードとその子ノードを比較し、子ノードの方が小さければ交換する。二つの子ノードを持つ場合には小さい方の子ノードと交換する。
- 交換した子ノードに移動して、親ノードとなる。親ノードの方が子ノードよりも小さいか、もしくはリーフに到達するまで手順(3)を繰り返す。すべてのノードを取り出したら終了する。
計算量
ヒープ・ソートは、ヒープのルートノードとヒープの最後のノードとの交換と、交換によって崩れたヒープの再ヒープ化の繰り返しによって行われます。これらの回数はノード数がn個ならばn-1回繰り返すことで完了します。ヒープのルートノードと最後のノードの交換の計算量は、n-1回の処理が行われることから、 \[O(n)\] となります。一方、再ヒープ化にかかる計算量は、対象となるヒープサイズが「ヒープのルートノードと最後のノードの交換」によって1ずつ減じられることから、各回ごとの計算量の合計として求める必要があります。1回当たりの計算量は、ルートに配置したノードがshift downによって一番下までずれた場合、木の高さをd、3つのノードからなる部分木の比較回数が2であることから、 \[ 2 \times d \] となります。完全二分木の場合、高さdにあるノードの数は\(2^d\)であることから \[ 2 \times d \times 2^d\] となります。オーダーは増加率の小さな項と係数を無視できることから、高さdにおける比較回数を\( d 2^d\)として、ヒープ全体におけるヒープ化の回数は、 \[ \sum_{i=1}^{d} i2^i = (d-1)2^{d+1} +2 \] ここで、ヒープサイズnと木の高さdとの関係が \(d = log(n+1) - 1\)であることから、 \[上式 < d(2^{d+1} - 1) \\ = n \cdot (\log(n+1) - 1) \] よってオーダーは、 \[O(n \log n)\] となります。ルートノードと最後のノードとの交換の計算量を合わせても、 \[O(n) + O(n \log n) \\ = O(n \log n)\] となります。
expand_lessBack to TOP